Zadania 7 i 8

Convergecast

W pracach do zadania 7. podjęto się analizy problemu convergecast w specjalnym ujęciu dla mechanizmów szybkiego wysyłania informacji o zagrożeniach. Uzyskano odpowiedzi dla ważnej, asynchronicznej wersji tego problemu oraz wskazano optymalne rozwiązania dla analizowanego modelu dla realistycznych parametrów (w tym dla rozmiaru sieci sensorycznej). Mechanizm convergecast (polska nazwa nie występuje w literaturze) jest przeciwieństwem mechanizmu rozgłaszania (ang. broadcast), czyli rozsyłania wiadomości od jednej stacji do wszystkich innych w jej zasięgu transmisyjnym. Zatem, rozpatrywany przypadek można opisać następująco: Dodatkowo, interesuje nas model bezprzewodowej, jednokanałowej sieci sensorycznej, a wraz z nim w obszar uwagi wchodzą następujące problemy: Z uwagi na powyższe założenia i problemy, w rozważaniach przyjęto następujące założenia: Algorytm, który podejmuje stacja sensoryczna w momencie wykrycia alarmu jest następujący: 

  Algorytm 1 Alarm dla stacji $s$
    $T = \frac{2N}{\log q N - \log\log f}$
    for $i=0$ to $d$
      $w[i] =$ losowa liczba rzeczywista z przedziału $(0,T)$
    posortuj tablicę $w[\,]$
    for $i=0$ do $d$
      czekaj na moment $w[i]$
      rozpocznij transmisję

Parametr $f$ jest czynnikiem kontrolującym prawdopodobieństwo dostarczenia wiadomości do stacji słuchającej. Poniżej przedstawiono podstawowe wyniki dla modelu asynchronicznego. Obliczenia przedstawiono na końcu raportu.
Zarys wyprowadzenia wyników
Dla zmiennych losowych $X_i, \ldots, X_N$ załóżmy że $X_{N+1} = 1$ oraz niech $L_1 = X_{(2)}-X_{(1)}, L_2 = X_{(3)}-X_{(2)}, \ldots, L_{N} = X_{(N+1)}-X_{(N)}$. Wtedy zachodzą następujące równania: \begin{equation} \label{eqn:maincond} \begin{aligned} & (L_1,L_2,\ldots,L_r) \stackrel{d}{=} (L_{\pi(1)}, L_{\pi(2)}, \ldots,L_{\pi(r)}) \mbox{ dla } r \leq N \\ & \Pr (L_1 > l_1, \ldots L_r > l_r) = (1 - l_1 - \ldots - l_r)^N_+\ . \end{aligned} \end{equation} gdzie $\pi$ jest dowolną permutacją $\{1,2,\ldots, r\}$. Dla binarnej zmiennej losowej $\xi_i$ określonej dla $i=1, \ldots, N$: \begin{equation*} \xi_i = \left\{ \begin{array}{ll} 1, & \mbox{jeżeli } L_i > \delta\\ 0, & \mbox{w p.p}. \end{array}\right. \end{equation*} można wyprowadzić poniższy lemat.

Lemat 1 Niech $\delta\in [0,1]$. Wtedy prawdopodobieństwo $\Pr(\xi_{1} = 1,\ldots,\xi_{k}=1,\xi_{k+1}=0,\ldots,\xi_{N}=0)$ wynosi \begin{equation} \sum_{i=0}^{N-k} \binom{N-k}{i}(-1)^i (1-\delta(i+k))^N_+ \end{equation}

\noindent Niech $S_i$ będzie binarną zmienną losową określoną dla $i=1,2,\ldots,N$ jak następuje: \begin{equation*} S_i = \left\{ \begin{array}{ll} 1, & \mbox{jeżeli } (\xi_1 = 1) \land (i=1) \lor (\xi_{i-1} \xi_{i} = 1) \land (2 \leq i \leq N)\\ 0, & \mbox{w p.p.} \end{array}\right. \end{equation*} Zmienna ta określa dla $i$-tej transmisji sukces, jeżeli $S_i = 1$.

Lemat 2 Prawdopodobieństwo że co najmniej jedna stacja transmitowała z powodzeniem wynosi \begin{equation*} \Pr(\sum_{i=1}^{N} S_i \geq 1) = 1- \sum_{k=0}^N \binom{N-k}{k} \sum_{i=0}^{N-k} \binom{N-k}{i}(-1)^i (1-\delta(i+k))^N_+ \end{equation*}

Lemat 3 Dla $\delta\in [1/2,1/2N]$ zachodzi następująca prawidłowość $$\Pr(\sum_{i=1}^{N} S_i \geq 1) \sim 1-(1-e^{-2 \delta N})^N.$$

Wprowadzona wyżej zmienna losowa $Z_i$ markuje te transmisje, które nie uległy zagłuszeniu jeśli $Z_i=1$. Wprowadźmy następującą binarną zmienną losową dla $i=1,2,\ldots,N$: \begin{equation*} S^Z_i = \left\{ \begin{array}{ll} 1, & \mbox{jeżeli } (Z_1 \xi_1 = 1) \land (i=1) \lor ((Z_{i-1} \xi_{i-1}) (Z_{i} \xi_{i}) = 1) \land (2 \leq i \leq N)\\ 0, & \mbox{w p.p.} \end{array}\right. \end{equation*} Teraz $S^Z_i=1$ oznacza, że $i$-ta transmisja została poprawnie odebrana \emph{pomimo} zakłóceń.

Lemat 4 Niech $0<\delta<1/(N-1)$. Wtedy prawdopodobieństwo $\Pr(Z_1 \cdot \xi_{1} = 1,\ldots, Z_k \cdot \xi_{k}=1,Z_{k+1} \cdot \xi_{k+1}=0,\ldots, Z_N \cdot \xi_{N}=0)$ wynosi \begin{equation*} \sum_{i=0}^{N-k} \binom{N-k}{i}(-1)^i q^{i+k} (1-\delta(i+k))^N_+ \end{equation*}

Lemat 5 \label{lemma:pst} Prawdopodobieństwo że co najmniej jedna stacja zakończyła transmisję z sukcesem wynosi \begin{align*} p_{q,\delta,N} & = \Pr(\sum_{i=1}^{N} S^Z_i \geq 1) = 1- \Pr(\sum_{i=1}^{N} S^Z_i = 0)\\ &= \sum_{k=0}^N \binom{N-k}{k} \sum_{i=0}^{N-k} \binom{N-k}{i}(-1)^i q^{i+k} (1-\delta(i+k))^N_+ \end{align*}

Lemat 6 Dla $0<\delta<1/(N-1)$ zachodzi $$\Pr(\sum_{i=1}^{N} S^Z_i \geq 1) \sim 1-(1-q^2 e^{-2 \delta N})^N.$$

Twierdzenie 1 Algorytm~\ref{alg:first} przesyła alarm z prawdopodobieństwem co najmniej $1-\frac{1}{f}$ w czasie $$\frac{2N}{\log(q^2 N) - \log(\log(f))}\Delta .$$

Twierdzenie 1 Jeśli liczba stacji $n$ jest większa niż $e \log(f)/q$, $d$ powinno spełniać zależność $n\cdot d \sim e \log(f)/q$.

Implementacja
W sieciach bezprzewodowych częstym zadaniem jest zbieranie lub agregacja danych zebranych przez poszczególne stacje i wysłanie ich bezpośrednio do jednej wyróżnionej stacji S. Operacja taka jest operacją odwrotną do rozgłaszania i nazywana jest convergecast. Głównym problemem przy zagadnieniu convergecast jest wybór właściwej strategii trasowania. Priorytetem dla stacji S jest maksymalizacja długości życia sieci, rozumiana jako liczba wykonań zadania zebrania danych z całej sieci, zanim któraś stacja zużyje całą swoją energię. W zadaniu 8 opracowano i zbadano właściwości algorytmu wyznaczania tras w sieci sensorycznej o nieregularnej strukturze. Prace podzielone były na etapy wymienione poniżej.
  1. Opracowanie i implementacja algorytmów wyboru trasy Optymalne rozwiązanie dla dowolnej sieci można znaleźć poprzez zastosowanie techniki programowania liniowego. Jest to niestety obarczone dużym wydatkiem obliczeniowym. Z uwagi na charakter urządzeń używanych w sieciach sensorycznych, taki poziom złożoności obliczeń optymalnego trasowania może być nie do przyjęcia. W związku z tym przeprowadzono analizę prostszych algorytmów, dających rozwiązanie suboptymalne, ale wymagające mniejszej mocy obliczeniowej. Opracowano następujące algorytmy trasowania pakietów:
    • ,,NSWE'', czyli algorytm najniższego sumarycznego wydatku energetycznego. Dla każdego węzła obliczana jest trasa do węzła S, która sumarycznie daje najniższy wydatek energetyczny. Wydatek ten liczony jest jako suma wydatków energetycznych poszczególnych węzłów w ścieżce, wynika z energii potrzebnej na transmisję do kolejnego węzła w ścieżce. Energia ta jest zależna od długoterminowej średniej tłumienia kanału radiowego pomiędzy poszczególnymi węzłami.
    • ,,NSWE zoptymalizowany'' – ścieżki wyznaczono w oparciu o algorytm NSWE, uzyskując tym samym wiedzę o obciążeniu energetycznym wszystkich węzłów w sieci. Następnie sprawdzano który węzeł jest najbardziej obciążony. Po znalezieniu takiego węzła część pakietów przez niego przechodzących była trasowana z jego ominięciem, tak, aby zmniejszyć jego wydatek energetyczny. Algorytm działa iteracyjnie do momentu znalezienie takiego rozwiązania, którego dalsze polepszenie poprzez omijanie węzła najbardziej obciążonego nie jest możliwe. Możliwe są dwa podejścia do omijania węzła najbardziej obciążonego:
    • dozwolone są przeskoki tylko do węzła S. Na poniższym schemacie, po lewej stronie, przedstawiono sytuację, gdy najbardziej obciążony był węzeł N6. Węzły N0 i N2, które na swoich ścieżkach mają węzeł N6, mogą podjąć decyzję o ominięciu węzła N6 i nadawaniu bezpośrednio do węzła S (metoda nazywana w tym dokumencie „NSWE optimized sink”).
    • dozwolone są przeskoki do dowolnego węzła, który na swojej ścieżce nie ma omijanego węzła. Poniższy schemat, po prawej stronie, obrazuje ominięcia najbardziej obciążonego węzła N6 przez węzły N0 i N2. Każdy z nich może nadawać do węzła S, ale też do innych węzłów, zarówno tych znajdujących się na jego ścieżce NSWE, ale za węzłem najbardziej obciążonym, lub do takich, które nie mają N6 na swojej ścieżce („NSWE optimized all”).
    • ,,NBB'' czyli algorytm wyznaczania ścieżki w taki sposób, jak w „nswe”, z tą różnicą, że każdy kolejny węzeł w ścieżce musiał znajdować się bliżej węzła S od węzła go poprzedzającego. Celem wprowadzenia tego algorytmu było zmniejszenie ilości obliczeń w stosunku do NSWE.
    • ,,NBB zoptymalizowane'' – algorytm optymalizacji taki sam, jak w analogicznym przypadku dla nswe. Tu również rozpatrzono dwie możliwości omijania węzła najbardziej obciążonego („NBB optimized sink” oraz „NBB optimized all”), działające tak samo, jako modyfikacje poprzedniego algorytmu.
      • \end{itemize}

                       

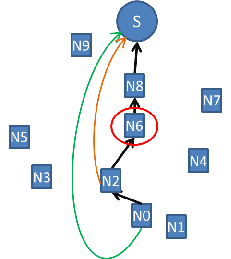
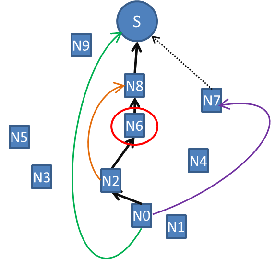
      Przykład optymalizacji wydatków energetycznych metodą ``NSWE optimized sink'' (lewy rysunek) oraz ``NSWE optimized all'' (prawy rysunek)

    • Symulacja działania algorytmu wraz z oceną jego właściwości W tej fazie przeprowadzono eksperymenty w celu zbadania właściwości ww. algorytmów, wykorzystując symulator opracowany w zadaniu 13. Jako referencję wykorzystano wyniki symulacji optymalnego rozwiązania, w którym wykorzystano programowanie liniowe.

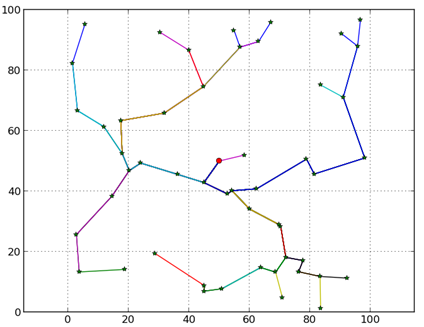
      Przykład sieci sensorycznej. Gwiazdkami oznaczono węzły sensoryczne, czerwona kropka symbolizuje węzeł centralny 'S', do którego spływają dane z pozostałych węzłów. Zaznaczono także przykładowe ścieżki transmisji.

      • Środowisko symulacyjne Symulacje algorytmów wykonano w sieci złożonej z $n$ węzłów sensorycznych, $n \in \{10, 20,$ $50, 100\}$, oraz jednego węzła centralnego $S$, do którego węzły sensoryczne adresują nadawane pakiety.
      • Złożoność obliczeniowa algorytmów Złożoność obliczeniowa była istotnym testem sprawności algorytmów zaproponowanych w tym zadaniu. Na załączonym poniżej wykresie przedstawiono zysk opisywanych algorytmów w stosunku do rozwiązania wykorzystującego programowanie liniowe, liczony jako stosunek czasu potrzebnego do obliczenia trasy optymalnej do czasu potrzebnego do obliczenia trasy przez zaproponowane algorytmy bazowe. Czas ten jest wprost proporcjonalny do liczby operacji, jakie muszą być wykonane przez urządzenie wyznaczające trasę, a więc dobrze obrazuje spadek zużycia energii. Dla przykładu, algorytm nbb wymaga około 10000 razy mniej obliczeń niż algorytm obliczający rozwiązanie optymalne.

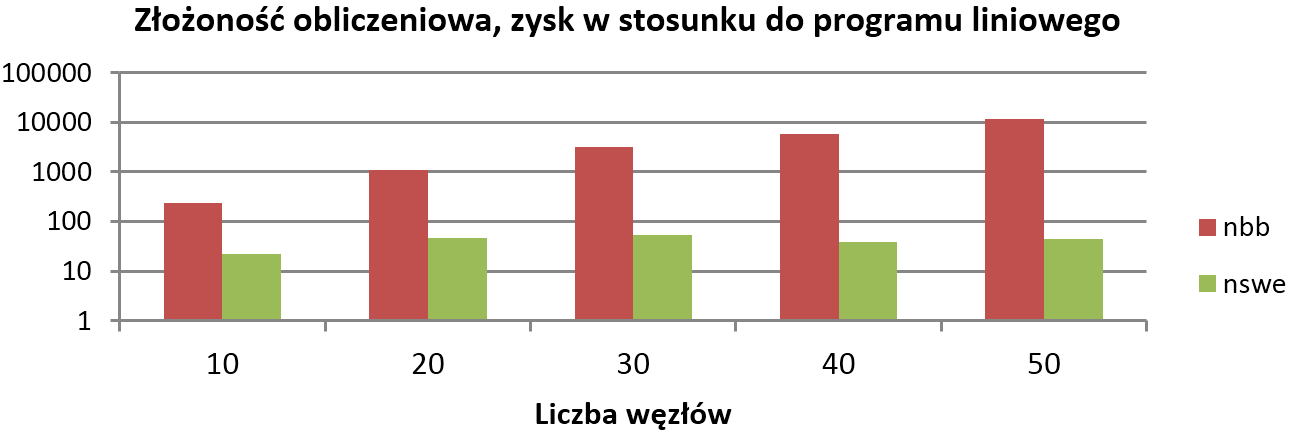
        Złożoność obliczeniowa algorytmów

      • Czas życia sieci i zużycie energii przez węzły W tym etapie skupiono się na analizie długości życia sieci, która jest odwrotnie proporcjonalna do zużycia energii przez najbardziej obciążony węzeł. Rozważania poszerzono o analizę zużycia energii przez wszystkie węzły transmisyjne. Na poniższych wykresach zaprezentowano przykładowe wyniki symulacji.

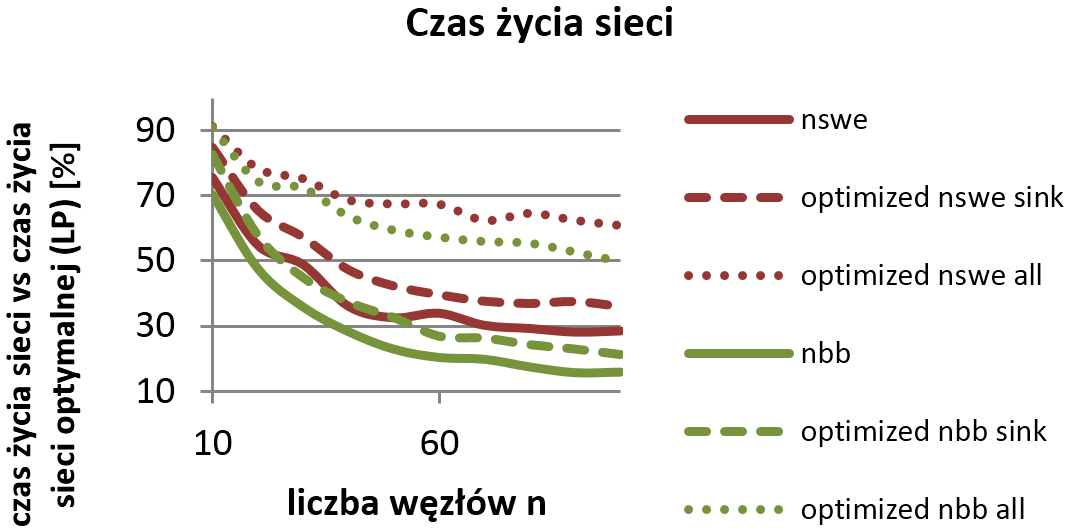
Czas życia sieci w stosunku do życia sieci optymalnej (wyznaczonej za pomocą programowania liniowego)

Pokazano, że dla niewielkich sieci czas życia może być bliski optymalnemu przy zastosowaniu uproszczonych algorytmów wyboru ścieżki. Dla większej ilości sensorów czas życia sieci w najlepszych z prezentowanych algorytmów stanowi 50-60\% wyniku rozwiązania optymalnego, przy czym w takich przypadkach wydatek związany z obliczeniem tras będzie wielokrotnie mniejszy. Zbadano obciążenie węzłów w poszczególnych algorytmach. Zaobserwowano, że optymalne rozwiązanie dążyło do zrównania wydatków energetycznych węzłów, podczas gdy rozwiązania suboptymalne powodowały mniejsze zużycie energii dla większości sensorów w sieci (nawet dla ok. 90\% węzłów), oczywiście poza węzłem najbardziej obciążonym. Rozwiązania suboptymalne będą powodować mniejsze obciążenie związane z obliczeniem ścieżek trasowania pakietów.