Zadanie 10

Relay nodes

Założenia

Sieci ze stacjami typu Relay będą istotnym elementem ekosystemów telekomunikacyjnych już w najbliższej przyszłości. Znajdują one zastosowanie zwłaszcza w sieciach sensorycznych, w których sensory mają ograniczoną moc nadawania. Przedmiotem rozważań w zadaniu 10 projektu ODOKRIM była optymalizacja mechanizmu współdzielenia zasobów w sieciach ze stacjami przekaźnikowymi. Z uwagi na istnienie dwóch rodzajów połączeń radiowych w sieciach z przekaźnikami, zagadnienie podziału zasobów radiowych można podzielić na dwa osobne przypadki:

• Współdzielenie zasobów w łączu między terminalem a węzłem pośredniczącym
• Współdzielenie zasobów w łączu pomiędzy węzłem pośredniczącym a kolejnym węzłem (w tym węzłem centralnym)

Podział zasobów w pierwszym z wymienionych przypadków może się odbywać z wykorzystaniem algorytmów opisanych w poprzednich zadaniach. Terminale mogą korzystać z przydzielonej im puli zasobów, używając algorytmu $\lambda$-ciągłego CSMA, unikając tym samym kolizji. Informacje o liczbie sensorów znajdujących się w obszarze pokrycia danej stacji przekaźnikowej mogą być uzyskiwane przy użyciu algorytmu zliczania zaproponowanego w zadaniu 3. Dane takie mogą służyć do określania zapotrzebowania na zasoby w łączu terminal – węzeł pośredniczący. W drugim z wymienionych wyżej problemów, węzeł centralny powinien dynamicznie zarządzać podziałem zasobów transmisyjnych pomiędzy podległe mu węzły pośredniczące. Zaletą zarządzania scentralizowanego jest możliwość zastosowania prostszych konstrukcyjnie terminali końcowych oraz stacji przekaźnikowych o małej mocy. Efektywność tego zarządzania ma kluczowe znaczenie dla jakości usług świadczonych w sieci. Przedmiotem większości prac w ramach zadania 10 było opracowanie odpowiedniego algorytmu. Badania rozpoczęto od określenia wymagań, jakie musi spełniać mechanizm współdzielenia zasobów, wśród nich m.in.:

• wsparcie dla różnego typu usług jednocześnie świadczonych w sieci
• dynamiczne dostosowanie się do zmiennego obciążenia poszczególnych węzłów sieci
• scentralizowane zarządzanie zasobami
• redukcja ruchu sygnalizacyjnego

Środowisko symulacyjne

Dla celów tego zadania zamodelowano sieć wieloskokową w strukturze drzewa, składającą się z jednego węzła centralnego, 42 węzłów pośredniczących oraz 126 węzłów sensorycznych. Schemat sieci zamieszczono na poniższym grafie

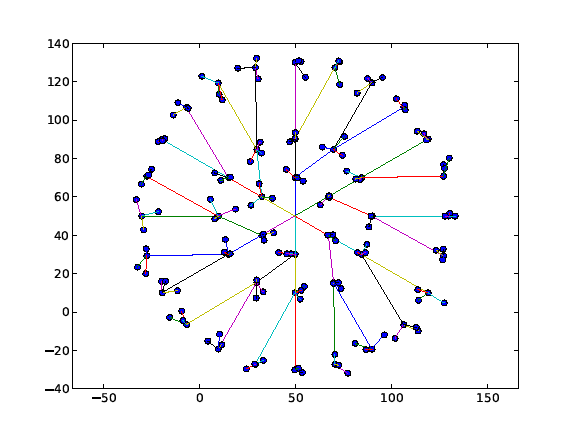
Schemat sieci użytej do symulacji.

Krawędzie oznaczają trasy, jakimi przebiega transmisja, przy czym zakłada się, że ścieżki transmisji mają charakter stały – nie ulegają zmianie w trakcie symulacji. Węzeł centralny znajduje się pośrodku. Węzły pośredniczące tworzą trzy okręgi, każdy węzeł pośredniczący z kręgu $n$ ($n \in \{1,2\}$) jest połączony z dwoma najbliższymi węzłami pośredniczącymi z kręgu $n+1$. Do każdego węzła pośredniczącego nadają bezpośrednio trzy węzły sensoryczne. Wiadomości w węzłach sensorycznych generowane są zgodnie z rozkładem Poissona. Pochodzą one z dwóch rodzajów serwisów o różnym dopuszczalnym czasie dotarcia wiadomości do węzła centralnego. Węzły pośredniczące wyposażone są w bufory typu FIFO, do których dodawane są kolejne pakiety transmitowane do danego węzła. Po przyznaniu zasobów transmisyjnych, węzeł pośredniczący wysyła pakiety z początku kolejki FIFO. W zadaniu badano zachowanie sieci w dwóch rodzajach symulacji reprezentujących różne obciążenie systemu.

Algorytm EDBP

W pierwszym kroku przeprowadzono analizę istniejących algorytmów, co pozwoliło na wyselekcjonowanie takich, których elementy mogły stanowić bazę dla nowego rozwiązania. Dalsze rozważania oparto o algorytm DBP (Delay-based Backpressure) [1], wprowadzając w nim kolejne modyfikacje. Zaproponowano nowy algorytm, nazwany EDBP (Enhanced Delay-based Backpressure), w którym węzeł centralny, na podstawie informacji od węzłów pośredniczących, przydziela im zasoby transmisyjne. W celu zaprezentowania algorytmu, załóżmy, że sieć może być przedstawiona jako skierowany graf $G=(V,E)$, gdzie $V$ oznacza zbiór węzłów, a $E$ oznacza zbiór łączy. Niech $K$ oznacza zbiór węzłów typu relay w sieci. Niech $Q_k$ oznacza bufor węzła $k$. Niech \begin{equation*} D_k = \max_{Q_k}( Z_{k,q} - Y_{k,q} ), \end{equation*} gdzie $Z_{k,q}$ to czas przebywania w sieci $q$-tego pakietu z bufora węzła $k$, a $Y_{k,q}$ to czas ważności $q$-tego pakietu z bufora węzła $k$ (wynikający z usługi, w ramach której przesyłany jest dany pakiet). Tak więc dla każdego pakietu w buforze węzła pośredniczącego określona zostanie różnica między czasem przebywania pakietu w sieci a czasem jego wygaśnięcia, a następnie dla każdego węzła wybrana będzie maksymalna taka wartość. W kolejnym kroku określona zostanie metryka opóźnienia, wg wzoru: \begin{equation*} \hat{D}_k = D_k - D_{k-1}, \end{equation*} gdzie węzeł $k$ to węzeł, do którego transmituje węzeł $k-1$. Tak więc $\hat{D}_k$ będzie reprezentowało różnicę między wartością $D$ dla danego węzła a wartością $D$ dla węzła go poprzedzającego. Następnie określony zostaje przyrost metryk opóźnienia, wg wzoru: \begin{equation*} \Delta \hat{D}_k = \hat{D}_k - \hat{D}_{k+1}, \end{equation*} Tak więc będzie on reprezentował różnicę między metrykami pomiędzy danym węzłem, a kolejnym węzłem. Węzły pośredniczące periodycznie wysyłają informacje o stanie swojego bufora. Informacja taka będzie się składać z dwóch elementów: $D_k$ oraz pozycję (indeks) $Idx$ pakietu najbardziej opóźnionego w buforze FIFO danego węzła. Węzeł centralny będzie obliczał przyrost metryk opóźnienia $\Delta\hat{D}_k$ przy założeniu znajomości tras w sieci. W symulacjach przyjęto, że transmisja jednego pakietu konsumuje jeden zasób transmisyjny. Przy założeniu że w danej chwili dostępnych jest $n$ zasobów, węzeł centralny rozdziela zasoby wg poniższego algorytmu:

Algorytm 1: Przydział zasobów
  Ustal pulę aktualnych zasobów $P \leftarrow n$
  Wybierz węzeł $W = \max_k(\Delta\hat{D}_k)$
  Przydziel węzłowi  liczbę zasobów = $\min(P,Idx)$
  $ P \leftarrow P - Idx $ 
  Jeśli $P \leq 0$ zakończ, w p.p. wróć do kroku 2

Algorytm ten porównano z algorytmem DBP [1]. Poniższy wykres przedstawia dystrybuantę czasu dostarczenia wiadomości do węzła centralnego dla obu algorytmów.

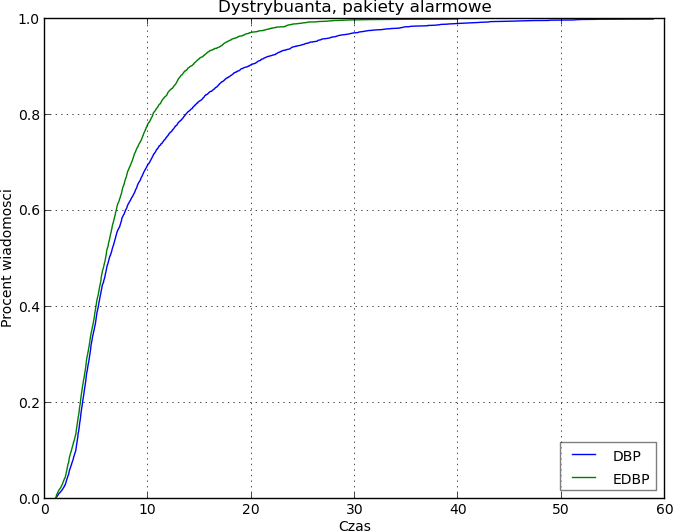
Dystrybuanta czasu dostarczenia wiadomości dla obu rozpatrywanych algorytmów.

Modyfikacje algorytmu EDBP W dalszej części zadania przeprowadzono szereg symulacji, w których sprawdzano wpływ następujących modyfikacji $\Delta\hat{D}_k$:

• uwzględnienie indeksu najbardziej opóźnionego pakietu. Celem było zwiększenie priorytetu tych węzłów, w których pakiety najbardziej opóźnione znajdują się na dalszych pozycjach w buforze. Przesłanie takiej wiadomości wymaga wcześniejszej transmisji dużej liczby pakietów, często w kilku iteracjach.
• uwzględnienie ilości skoków pozostałych do węzła docelowego. Celem było zwiększanie priorytetu węzłów znajdujących się dalej od węzła docelowego (odległości rozumianej jako ilość skoków do węzła centralnego). Im dalej dany węzeł znajduje się od węzła docelowego, tym bardziej pakiety znajdujące się w jego buforze narażone są na przekroczenie maksymalnego opóźnienia określonego przez usługę w ramach której są przesyłane. Zaproponowana modyfikacja miała na celu uwzględnienie tego faktu.
• zwiększenie w metryce wagi informacji o obciążeniu bieżącego węzła. Modyfikacja ma na celu zwiększenie efektywności algorytmu w sytuacji gdy cały potok od sensora do węzła centralnego (węzeł bieżący, poprzedni i następny) jest mocno obciążony - na przykład gdy sensory z pewnego obszaru wysyłają w danej chwili więcej komunikatów niż sensory w pozostałej części sieci.

Wyniki analizy eksperymentalnej

Przedstawione w raporcie wyniki symulacji pokazują, że nowy algorytm EDBP spełnia postawione przed nim założenia i lepiej zarządza współdzieleniem zasobów radiowych w sieci, szczególnie w przypadku pakietów o większych wymaganiach co do opóźnienia, zmniejszając liczbę przeterminowanych pakietów o ponad 30\%. Uwzględnienie w metryce indeksu najbardziej opóźnionego pakietu przynosi poprawę w mocno obciążonej sieci. Zwiększenie wagi informacji o obciążeniu bieżącego węzła z kolei przynosi największe korzyści dla mocno opóźnionych pakietów. Uwzględnienie ilości skoków w metryce nie przyniosło zadowalających zysków. Źródła: [1] - Bo Ji; Changhee Joo; Shroff, N.B. ,,Delay-based Back-Pressure scheduling in multi-hop wireless networks,'' INFOCOM, 2011 Proceedings IEEE