Narzędzia On-Line
W sieci można znaleźć wiele dostępnych dla każdego bardzo dobrych narzędzi ułatwiających wykonywanie obliczeń matematycznych. Za ich pomocą możesz sprawdzić poprawność rozwiązań większości typowych zadań z podstawowych przedmiotów matematycznych na studiach. Oto kilka z nich:
 Na stronie Wolfram Alpha możesz przeprowadzić wiele, nawet
bardzo zaawansowanych, obliczeń. Oto kilka przykładów użycia:
Na stronie Wolfram Alpha możesz przeprowadzić wiele, nawet
bardzo zaawansowanych, obliczeń. Oto kilka przykładów użycia:
- granica ciągu an = (1-1/n)n:
lim (1-1/n)^n as n->infinity - granica funkcji:
lim (cos(x) - 1)/x^2 as x->0 - wykres funkcji:
plot x^3 -2 x^2+ 1 - całka nieoznaczona:
integrate x sin(x) dx - całka oznaczona:
integrate x^2 dx from x=0 to 1 - Więcej
 Za pomocą wyszukiwarki Google możesz generować wykresy prostych funkcji jednej zmiennej.
Na przykład, wprowadź w pole zapytań wzór
x^2/(1+x^2).
Za pomocą wyszukiwarki Google możesz generować wykresy prostych funkcji jednej zmiennej.
Na przykład, wprowadź w pole zapytań wzór
x^2/(1+x^2).
Możesz również wprowadzić jednocześnie kilka wzorów, np.
sin(x)/x, 1 - x^2/6+x^4/120
oddzielając je przecinkiem.
Możesz również ograniczyć wyświetlany obszar poleceniem x is from a to b, np.
x/(1+x^2), x is from -10 to 10, y is from -1 to 1
Jeśli używasz przeglądarki która obsługuje technologię
WebGL
i masz stosunkowo nową kartę graficzną,
to możesz również narysować wykres funkcji dwóch zmiennych, np.
x^2+y^2.
Wypróbuj następująca funkcję:
5 + (-sqrt(1-x^2-(y-abs(x))^2))*cos(30*((1-x^2-(y-abs(x))^2))), x is from -1 to 1, y is from -1 to 1.5, z is from 1 to 6
 Kalkulator pochodnych ze strony
www.derivative-calculator.net/
pozwala na obliczanie pochodnej szerokiej klasy funkcji w trybie on-line.
Potrafi również liczyć pochodne cząstkowe.
Za jego pomocą możesz sprawdzić poprawność swoich rozwiązań -
pokazuje również pośrednie kroki obliczeń.
Kalkulator pochodnych ze strony
www.derivative-calculator.net/
pozwala na obliczanie pochodnej szerokiej klasy funkcji w trybie on-line.
Potrafi również liczyć pochodne cząstkowe.
Za jego pomocą możesz sprawdzić poprawność swoich rozwiązań -
pokazuje również pośrednie kroki obliczeń.
 Kalkulator całek ze strony
www.integral-calculator.com
pozwala na obliczanie całek oznaczonych i nieoznaczonych z szerokiej klasy funkcji w trybie on-line.
Kalkulator całek ze strony
www.integral-calculator.com
pozwala na obliczanie całek oznaczonych i nieoznaczonych z szerokiej klasy funkcji w trybie on-line.
Pamiętaj o zachowaniu ostrożności przy posługiwaniu się tymi narzędziami. Oto przykład: na lewym rysunku znajduje się wykres funkcji $f(x) = e^{x} \ln(1+e^{-x})$ wygenerowany przez program Mathematica (luty, 2013) a na prawym rysunku znajduje się poprawny wykres tej funkcji.
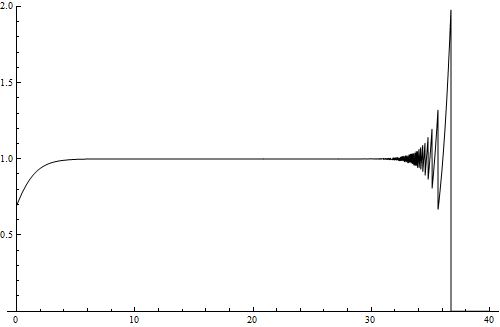
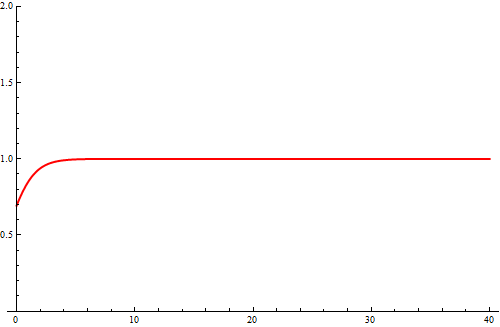
Błąd ten łatwo zauważyć jeśli policzy się granicę funkcji $f$ przy x dążącym do nieskończoności, co można zrobić korzystając z reguły de l'Hospitala: $$ \lim_{x\to\infty} f(x) = \lim_{x\to\infty} \frac{\ln(1+e^{-x})}{e^{-x}} =^{H} \lim_{x\to\infty} \frac{e^{-x}}{(1+e^{-x}) e^{-x}} = \lim_{x\to\infty} \frac{1}{1+e^{-x}} = 1~. $$ Nieco dokładniejsza obliczenia pokazują, że $|f(x)-1|\lt e^{-x}$, więc, np., dla $x \gt 20$ mamy $|f(x)-1| \lt 2.1 \times 10^{-9}$. Błąd jest spowodowany tym, że dla wartości x większych od 30 zaczynają narastać błędy numeryczne związane z wyznaczaniem wartości $f(x)$.