Dzień liczby PI
O dniu liczby $\pi$
Od roku 1988 w dniu 14 marca obchodzimy Dzień Liczby $\pi$.
$\pi$ = 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 51 32 823 066 470 938 446 095 505 822 317 253 594 081 284 811 174 502 841 027 019 385 211 055 596 446 229 489 549 303 819 644 288 109 756 659 334 461 284 756 482 337 867 831 652 712 019 091 456 485 669 234 603 486 104 543 266 482 133 936 072 602 491 412 ....
Kilka przybliżeń liczby $\pi$ ułamkami
- $\frac{22}{7}$ = 3.14285714285714…
- $\frac{333}{106}$ = 3.14150943396226…
- $\frac{355}{113}$ = 3.14159292035398…
Kilka wzorów w których występuje liczba $\pi$
Starożytność
- obwód koła o promieniu r: $ L =2 \pi r $
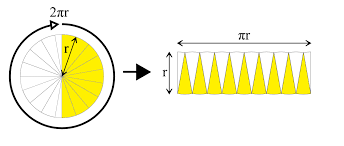
- Archimedes: pole koła o promieniu r: $ S = \pi r^2 $
- Archimedes: powierzchnia kuli o promieniu r: $S = 4 \pi r^2$
- Archimedes: objętość kuli o promieniu r: $V = \frac{4}{3} \pi r^3$
Nowożytność
- Stirling, ok. 1730: $n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$
- Euler, 1735: $\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}$
- Euler, ok. 1740: $e^{\pi i} + 1 = 0$
- Lambert, 1761: liczba $\pi$ jest niewymierna
- Laplace (1778) $\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}$
- Lindemann, 1882: liczba $\pi$ jest przestępna
- Plouffe, 1995: $ \pi = \sum_{n=0}^{\infty} \frac{1}{16^n}(\frac{4}{8n+1} - \frac{2}{8n+4} - \frac{1}{8n+5} - \frac{1}{8n+6})$
Jeśli chcesz sprawdzić, czy Twoja data urodzin występuje w ciągu pierwszych 200 mln cyfr liczby $\pi$ to odwiedź stronę PiQuery.