On-Line Tools
On the web you can find many very good tools that make it easy perform mathematical calculations. Using these tools, you can check the solutions most common tasks of basic math courses. Here are some of them:
On the page Wolfram Alpha you can perform many even very advanced calculations.
Here are some examples:
- limit of the sequenceu an = (1-1/n)n:
lim (1-1/n)^n as n->infinity - limit of a function:
lim (cos(x) - 1)/x^2 as x->0 - graph of a function:
plot x^3 -2 x^2+ 1 - undefinite integral:
integrate x sin(x) dx - definite integral:
integrate x^2 dx from x=0 to 1 - more
Using the Google search engine you can generate graphs of simple functions of one variable. For example, enter the query
x^2/(1+x^2).
You can also enter at the same time a few formulas:
sin(x)/x, 1 - x^2/6+x^4/120
separating them with a comma.
You can also restrict the display area using the command x is from a to b:
x/(1+x^2), x is from -10 to 10, y is from -1 to 1
If you use a browser that supports WebGL and you have a relatively new graphics card, you can also draw a graph of a function of two variables, eg
x^2+y^2.
Try the following function:
5 + (-sqrt(1-x^2-(y-abs(x))^2))*cos(30*((1-x^2-(y-abs(x))^2))), x is from -1 to 1, y is from -1 to 1.5, z is from 1 to 6
Calculator from the page
www.derivative-calculator.net/
allows you to calculate on-line derivatives of a wide class of functions.
It can also count the partial derivatives. This tool shows also the intermediate steps of calculation.
Calculator of integrals from
www.integral-calculator.com
allows you to calculate on-line definite and indefinite integrals from a wide class of functions.
However, be careful Here is an example: in the left figure you have the graph of the function $f (x) = e ^ {x} \ln (1 + e ^{-x}) $ generated by Mathematica (February, 2013) and on the the right figure you have the correct graph of this function.
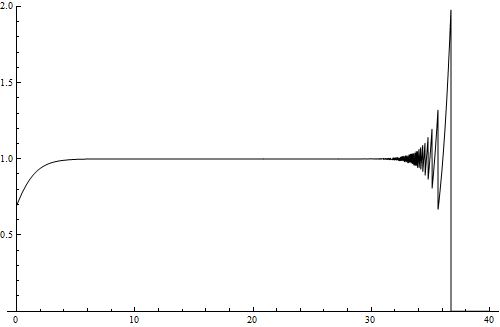
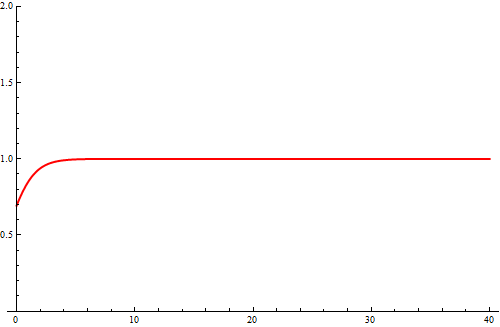
It is easy to see this error if you calulate the limit of the function $f$ at infinity. This can be done with the l'Hospital rule: $$ \lim_{x\to\infty} f(x) = \lim_{x\to\infty} \frac{\ln(1+e^{-x})}{e^{-x}} =^{H} \lim_{x\to\infty} \frac{e^{-x}}{(1+e^{-x}) e^{-x}} = \lim_{x\to\infty} \frac{1}{1+e^{-x}} = 1~. $$ Slightly more precise calculations show that $|f(x)-1|\lt e^{-x}$, so, for example, for $x \gt 20$ we have $|f(x)-1| \lt 2.1 \times 10^{-9}$. The error is caused by the fact that for values of x greater than 30 the numerical errors associated with the assignment of $f(x)$ starts rapidly increase.