Zegarek binarny

P1. Układy pozycyjne

1. Poznaliśmy regułę podzielności przez 9 liczb zapisanych w układzie dziesiętnym: $$9|(a_n\ldots a_2a_1a_0)_{(10)} \equiv 9|(a_0+a_1+\ldots +a_n)$$
2. Nauczyliśmy się zapisywać liczby w układzie dwójkowym, np. $13 = (1101)_{(2)}$, $14 = (1110)_{(2)}$, $15 = (1111)_{(2)}$
3. Omówiliśmy algorytm na wyznaczanie reprezentacji dwójkowej danej liczby naturalnej dodatniej. Oto "pseudo-kod" tego algorytmu:

   FUNCTION ToBin(int n) {
     string s = "";
     WHILE (n>0) {
       IF (n % 2 == 0){
         s = "0" + s;
       } ELSE {
         s = "1" + s;
   	}
       n = n/2;
     }
     RETURN s;
   }
   

   Zaczęliśmy przekształcać ten "pseudo-kod" na kod w języku C++. Będziemy go ulepszać na następnych zajęciach.

Zadania po pierwszych zajęciach

1. Sformułuj i udowodnij zasadę podzielności przez liczbę 3 liczb zapisanych w układzie dziesiętnym.
2. Zapisz wiek swojej mamy, taty, rodzieństwa w układzie dwójkowym
3. Doprowadź algorytm który zaczęliśmy pisać do postaci kompilowalnej

P1. Równanie ruchu w polu centralnym

Rozważamy obiekt punktowe znadujący się w centralnym polu grawitacyjnym. Jego położenie w chwili $t$ jest opisywane przez współrzędne $(x(t),y(t))$, a prędkość przez wektor $(v_x(t),v_y(t))$. Korzystając z tego, że $v(t) = \frac{\Delta s}{\Delta t}$, $a(t) = \frac{\Delta v}{\Delta t}$, $F = m\cdot a$ oraz $F = G \frac{M \cdot m}{r^2}$ wyprowadziliśmy następujące równania ruchu:

1. $x(t+\delta) = x(t) + v_x(t) \cdot \delta$
2. $y(t+\delta) = y(t) + v_y(t) \cdot \delta$
3. $v_x(t+\delta) = v_x(t) - \frac{ C \cdot x(t) \cdot \delta}{(x(t)^2+y(t)^2)^{3/2}}$
4. $v_y(t+\delta) = v_y(t) - \frac{ C \cdot y(t) \cdot\delta}{(x(t)^2+y(t)^2)^{3/2}}$

(gdzie $C = G\cdot M$). Następnie zaprogramowaliśmy symulator ruchu w programie Excel (mimo, iż nie jest to idealne narzędzie do tego celu). Oto co otrzymaliśmy:

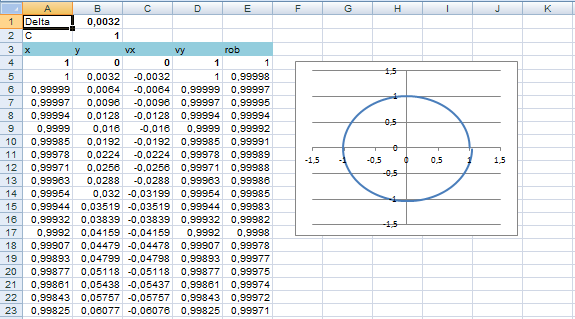
W komórkę E4 wstawiliśmy formułę =\$B\$2/POTĘGA(A4*A4+B4*B4;3/2). W komórkach A5, B5, C5, D5, E5 wstawiliśmy następujące formuły: =A4+C4*\$B\$1, =B4+D4*\$B\$1, =C4-A4*E4*\$B\$1, =D4-B4*E4*\$B\$1, =\$B\$2/POTĘGA(A5*A5+B5*B5;3/2). Nastepnie blok A5-E5 skopiowaliśmy 2 tysiące razy (w dół). Nastepnie zaznaczyliśmy blok A4-B2000 z wygenerowaliśmy wykres punktowy. A potem bawiliśmy się zmianą parametrów Delta oraz vy. Zaobserwowaliśmy ruch eliptyczny, paraboliczny i hiperboliczny.

Naszym kolejnym celem będzie zaimplementowanie tych równań w języku Java.