Algorytm = Logika + Sterowanie
Relacje, funkcje i niedeterminizm
10/07/13 15:02
Najważniejszą cechą odróżniającą programowanie w Prologu od programowania funkcyjnego jest wyrażanie w nim relacji a nie jedynie funkcji (każda funkcja jest relacją ale nie każda relacja jest funkcją).
Po lewej stronie przedstawiono relację R będącą podzbiorem iloczynu kartezjańskiego X×Y, natomiast po prawej stronie przedstawiono funkcję F:X →Y, która również jest relacją zawartą w zbiorze X×Y:
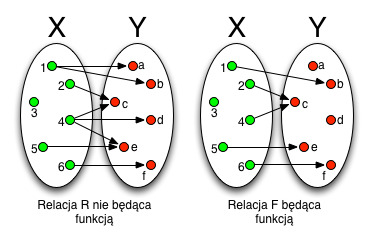
Relacja R i funkcja F, to zbiory uporządkowanych par elementów:
R = {(1, a), (1, b), (2, c), (4, c), (4, d), (4, e), (5, e), (6, f)}
F = {(1, b), (2, c), (4, c), (5, e), (6, f)}
W funkcji F nie ma dwóch par (x, y1) i (x, y2) o tym samym pierwszym elemencie x ale dwóch różnych drugich elementach y1 i y2, natomiast w relacji R są takie pary np. (1, a) i (1, b).
Relację R można wyrazić w Prologu w postaci następujących faktów:
r(1, a).
r(1, b).
r(2, c).
r(4, c).
r(4, e).
r(5, e).
r(6, f).
Jeśli zadamy Prologowi pytanie:
?- r(2, X).
X = c.
to otrzymamy tylko jedną odpowiedź X = c, ponieważ w relacji R jest tylko jedna para z pierwszym elementem równym 2.
Jeśli jednak zadamy pytanie z pierwszym elementem równym 4, to otrzymamy dwie odpowiedzi:
?- r(4, X).
X = c ;
X = e ;
false.
O warunku, który dostarcza więcej niż jedną odpowiedź mówimy, że jest niedeterministyczny.
Uwaga: nie oznacza to, że jest losowy ale to, że może być wyprowadzony na więcej niż jeden sposób.
Wyrażanie relacji, a nie jedynie funkcji, umożliwia Prologowi w prosty sposób wnioskowanie o relacji odwrotnej czyli poszukiwanie pierwszych elementów par przy zadanym drugim ich elemencie:
?- r(X, e).
X = 4 ;
X = 5.
Jak widać nie ma potrzeby definiowania w Prologu relacji odwrotnej do R. Wystarczy zadać pytanie ze zmienną na odpowiedniej pozycji.
W przypadku programowania funkcyjnego nie jest to możliwe. Wymagałoby to zdefiniowania nowej funkcji odwrotnej a takowa może w ogóle nie istnieć (funkcja odwrotna istnieje tylko dla funkcji różnowartościowych).
Taka „prologowa” symetria w pytaniach kończy się z chwilą skorzystania z predykatów wyliczających wartości wyrażeń arytmetycznych. Otóż wymóg wcześniejszego podstawienia wartości pod wszystkie zmienne występujące w wyrażeniu narzuca jeden kierunek obliczeń.
Przykład: predykat =:= sprawdza równość dwóch arytmetycznych wyrażeń. Nie wyliczy on jednak wartości zmiennej X z tak prostego równania:
?- 2 + X =:= 4.
ERROR: =:=/2: Arguments are not sufficiently instantiated
Zaradzić temu można jedynie przez skorzystanie z programowania z więzami (przykład w SWI-Prologu):
?- use_module(library(clpfd)).
% library(occurs) compiled into occurs 0.00 sec, 14 clauses
% library(apply_macros) compiled into apply_macros 0.00 sec, 41 clauses
% library(assoc) compiled into assoc 0.00 sec, 97 clauses
% library(pairs) compiled into pairs 0.00 sec, 22 clauses
% library(clpfd) compiled into clpfd 0.10 sec, 2,615 clauses
true.
?- 2 + X #= 4.
X = 2.
Bardziej interesującym przykładem warunku niedeterministycznego jest zapytanie o to na jakie sposoby można rozerwać listę [1, 2, 3]:
?- append(X, Y, [1, 2, 3]).
X = [],
Y = [1, 2, 3] ;
X = [1],
Y = [2, 3] ;
X = [1, 2],
Y = [3] ;
X = [1, 2, 3],
Y = [] ;
false.
Skąd ten niedeterminizm? Przyjrzyjmy się definicji predykatu append/3:
append([], A, A).
append([A|B], C, [A|D]) :-
append(B, C, D).
Jeśli w pytaniu o warunek append na pierwszej pozycji podamy zmienną a na trzeciej zmienną lub listę różną od pustej, to Prolog będzie mógł skorzystać w pierwszym kroku wnioskowania zarówno z pierwszej jak i drugiej klauzuli. Można zatem sobie wyobrażać, że wśród udzielonych odpowiedzi znajdą się te, które uzyskano gdy w pierwszym kroku skorzystano z pierwszej klauzuli oraz te, które uzyskano gdy skorzystano z drugiej klauzuli.
Mój ulubiony przykład niedeterministycznego warunku, to select(a, X, [1, 2, 3]):
?- select(a, X, [1, 2, 3]).
X = [a, 1, 2, 3] ;
X = [1, a, 2, 3] ;
X = [1, 2, a, 3] ;
X = [1, 2, 3, a] ;
false.
Chociaż nazwa predykatu select(A, L1, L2) sugeruje, że wyjmuje on element A z listy L1 i dostarcza listę pozostałych elementów L2, to jednak dzięki niedeterminizmowi i temu, że select/3 wyraża relację między elementem a dwoma listami, może posłużyć on do wkładania wartości na listę, i to na wszystkie możliwe pozycje.
Wykorzystując predykat select/3 można w prosty sposób napisać predykat wyrażający relację jaka zachodzi między listą a jej permutacją:
perm([], []).
perm(L1, [A | L2]) :-
select(A, L1, L3),
perm(L3, L2).
Dzięki niedeterminizmowi możemy generować kolejne permutacje:
?- perm([1, 2, 3], X).
X = [1, 2, 3] ;
X = [1, 3, 2] ;
X = [2, 1, 3] ;
X = [2, 3, 1] ;
X = [3, 1, 2] ;
X = [3, 2, 1] ;
false.
Nie jest prawdą, że powyższy predykat perm/2 pozwala na zadawanie mu symetrycznego pytania:
?- perm(X, [1, 2, 3]).
X = [1, 2, 3] ;
ERROR: Out of global stack
Ale o tym przy przy innej okazji…
Po lewej stronie przedstawiono relację R będącą podzbiorem iloczynu kartezjańskiego X×Y, natomiast po prawej stronie przedstawiono funkcję F:X →Y, która również jest relacją zawartą w zbiorze X×Y:

Relacja R i funkcja F, to zbiory uporządkowanych par elementów:
R = {(1, a), (1, b), (2, c), (4, c), (4, d), (4, e), (5, e), (6, f)}
F = {(1, b), (2, c), (4, c), (5, e), (6, f)}
W funkcji F nie ma dwóch par (x, y1) i (x, y2) o tym samym pierwszym elemencie x ale dwóch różnych drugich elementach y1 i y2, natomiast w relacji R są takie pary np. (1, a) i (1, b).
Relację R można wyrazić w Prologu w postaci następujących faktów:
r(1, a).
r(1, b).
r(2, c).
r(4, c).
r(4, e).
r(5, e).
r(6, f).
Jeśli zadamy Prologowi pytanie:
?- r(2, X).
X = c.
to otrzymamy tylko jedną odpowiedź X = c, ponieważ w relacji R jest tylko jedna para z pierwszym elementem równym 2.
Jeśli jednak zadamy pytanie z pierwszym elementem równym 4, to otrzymamy dwie odpowiedzi:
?- r(4, X).
X = c ;
X = e ;
false.
O warunku, który dostarcza więcej niż jedną odpowiedź mówimy, że jest niedeterministyczny.
Uwaga: nie oznacza to, że jest losowy ale to, że może być wyprowadzony na więcej niż jeden sposób.
Wyrażanie relacji, a nie jedynie funkcji, umożliwia Prologowi w prosty sposób wnioskowanie o relacji odwrotnej czyli poszukiwanie pierwszych elementów par przy zadanym drugim ich elemencie:
?- r(X, e).
X = 4 ;
X = 5.
Jak widać nie ma potrzeby definiowania w Prologu relacji odwrotnej do R. Wystarczy zadać pytanie ze zmienną na odpowiedniej pozycji.
W przypadku programowania funkcyjnego nie jest to możliwe. Wymagałoby to zdefiniowania nowej funkcji odwrotnej a takowa może w ogóle nie istnieć (funkcja odwrotna istnieje tylko dla funkcji różnowartościowych).
Taka „prologowa” symetria w pytaniach kończy się z chwilą skorzystania z predykatów wyliczających wartości wyrażeń arytmetycznych. Otóż wymóg wcześniejszego podstawienia wartości pod wszystkie zmienne występujące w wyrażeniu narzuca jeden kierunek obliczeń.
Przykład: predykat =:= sprawdza równość dwóch arytmetycznych wyrażeń. Nie wyliczy on jednak wartości zmiennej X z tak prostego równania:
?- 2 + X =:= 4.
ERROR: =:=/2: Arguments are not sufficiently instantiated
Zaradzić temu można jedynie przez skorzystanie z programowania z więzami (przykład w SWI-Prologu):
?- use_module(library(clpfd)).
% library(occurs) compiled into occurs 0.00 sec, 14 clauses
% library(apply_macros) compiled into apply_macros 0.00 sec, 41 clauses
% library(assoc) compiled into assoc 0.00 sec, 97 clauses
% library(pairs) compiled into pairs 0.00 sec, 22 clauses
% library(clpfd) compiled into clpfd 0.10 sec, 2,615 clauses
true.
?- 2 + X #= 4.
X = 2.
Bardziej interesującym przykładem warunku niedeterministycznego jest zapytanie o to na jakie sposoby można rozerwać listę [1, 2, 3]:
?- append(X, Y, [1, 2, 3]).
X = [],
Y = [1, 2, 3] ;
X = [1],
Y = [2, 3] ;
X = [1, 2],
Y = [3] ;
X = [1, 2, 3],
Y = [] ;
false.
Skąd ten niedeterminizm? Przyjrzyjmy się definicji predykatu append/3:
append([], A, A).
append([A|B], C, [A|D]) :-
append(B, C, D).
Jeśli w pytaniu o warunek append na pierwszej pozycji podamy zmienną a na trzeciej zmienną lub listę różną od pustej, to Prolog będzie mógł skorzystać w pierwszym kroku wnioskowania zarówno z pierwszej jak i drugiej klauzuli. Można zatem sobie wyobrażać, że wśród udzielonych odpowiedzi znajdą się te, które uzyskano gdy w pierwszym kroku skorzystano z pierwszej klauzuli oraz te, które uzyskano gdy skorzystano z drugiej klauzuli.
Mój ulubiony przykład niedeterministycznego warunku, to select(a, X, [1, 2, 3]):
?- select(a, X, [1, 2, 3]).
X = [a, 1, 2, 3] ;
X = [1, a, 2, 3] ;
X = [1, 2, a, 3] ;
X = [1, 2, 3, a] ;
false.
Chociaż nazwa predykatu select(A, L1, L2) sugeruje, że wyjmuje on element A z listy L1 i dostarcza listę pozostałych elementów L2, to jednak dzięki niedeterminizmowi i temu, że select/3 wyraża relację między elementem a dwoma listami, może posłużyć on do wkładania wartości na listę, i to na wszystkie możliwe pozycje.
Przypomina mi to scenę z komedii Seks nocy letniej, w której główny bohater, będący wynalazcą, opowiada o swoim urządzeniu do wyciągania ości z ryby oraz, co jest mniej praktyczne, mogącym również wkładać ości w rybę.
Wykorzystując predykat select/3 można w prosty sposób napisać predykat wyrażający relację jaka zachodzi między listą a jej permutacją:
perm([], []).
perm(L1, [A | L2]) :-
select(A, L1, L3),
perm(L3, L2).
Dzięki niedeterminizmowi możemy generować kolejne permutacje:
?- perm([1, 2, 3], X).
X = [1, 2, 3] ;
X = [1, 3, 2] ;
X = [2, 1, 3] ;
X = [2, 3, 1] ;
X = [3, 1, 2] ;
X = [3, 2, 1] ;
false.
Nie jest prawdą, że powyższy predykat perm/2 pozwala na zadawanie mu symetrycznego pytania:
?- perm(X, [1, 2, 3]).
X = [1, 2, 3] ;
ERROR: Out of global stack
Ale o tym przy przy innej okazji…