Algorytm = Logika + Sterowanie
Co to jest Prolog?
Prolog jest językiem programowania.
Mówi się, że jest on językiem deklaratywnym. Oznacza to, że nie zapisuje się w nim algorytmu rozwiązującego problem. Zamiast tego opisuje się problem tak aby system mógł sam wywnioskować jakie jest rozwiązanie zdefiniowanego problemu.
Zatem w Prologu wyraża się CO chce się rozwiązać a nie JAK się to rozwiązuje.
Nazwa języka Prolog to akronim od PROgramowanie w LOGice (fr. programmation en logique, ang. programming in logic).
Program w Prologu składa się z logicznych formuł opisujących własności problemu. System Prolog stosując metodę rezolucji wnioskuje na podstawie tego opisu jaka jest odpowiedź na zadane pytanie (rozwiązanie problemu).
Tak jak Niklaus Wirth zapisał w tytule swojej książki równanie opisujące czym są programy:
ALGORYTMY + STRUKTURY DANYCH = PROGRAMY,
tak Robert Kowalski sformułował tytuł swojego artykułu w postaci następującego równania:
ALGORYTM = LOGIKA + STEROWANIE,
które należy rozumieć w ten sposób, że do wyrażenia algorytmu wystarczy logiczny opis problemu a wnioskowanie zamieszczone w systemie (sterowanie), znajdzie rozwiązanie problemu.
Mówi się, że jest on językiem deklaratywnym. Oznacza to, że nie zapisuje się w nim algorytmu rozwiązującego problem. Zamiast tego opisuje się problem tak aby system mógł sam wywnioskować jakie jest rozwiązanie zdefiniowanego problemu.
Zatem w Prologu wyraża się CO chce się rozwiązać a nie JAK się to rozwiązuje.
Nazwa języka Prolog to akronim od PROgramowanie w LOGice (fr. programmation en logique, ang. programming in logic).
Program w Prologu składa się z logicznych formuł opisujących własności problemu. System Prolog stosując metodę rezolucji wnioskuje na podstawie tego opisu jaka jest odpowiedź na zadane pytanie (rozwiązanie problemu).
Tak jak Niklaus Wirth zapisał w tytule swojej książki równanie opisujące czym są programy:
ALGORYTMY + STRUKTURY DANYCH = PROGRAMY,
tak Robert Kowalski sformułował tytuł swojego artykułu w postaci następującego równania:
ALGORYTM = LOGIKA + STEROWANIE,
które należy rozumieć w ten sposób, że do wyrażenia algorytmu wystarczy logiczny opis problemu a wnioskowanie zamieszczone w systemie (sterowanie), znajdzie rozwiązanie problemu.
Stałe i zmienne
Najprostsze dane w Prologu wyraża się za pomocą stałych.
Stałe zapisuje się w postaci ciągu liter i cyfr rozpoczynających się małą literą:
Szczególnymi stałymi są liczby:
Zmienne zapisuje się w postaci ciągu liter i cyfr rozpoczynających się wielką literą:
Szczególną rolę odgrywa w Prologu zmienna o nazwie _ (podkreślenie) i oznacza ona dowolną ale nieistotną wartość.
Stałe zapisuje się w postaci ciągu liter i cyfr rozpoczynających się małą literą:
- null
- p1
- kwadrat
Szczególnymi stałymi są liczby:
- 10
- 3.14
- 1e-6
Zmienne zapisuje się w postaci ciągu liter i cyfr rozpoczynających się wielką literą:
- X
- WysokoscProstokata
- P123
Szczególną rolę odgrywa w Prologu zmienna o nazwie _ (podkreślenie) i oznacza ona dowolną ale nieistotną wartość.
Termy
Termami nazywamy w Prologu wyrażenia, przy czym mogą one być proste lub złożone.
Termy proste to stałe i zmienne.
Termy złożone buduje się łącząc pewną liczbę termów w jeden.
Do łączenia służą funktory, które - podobnie jak stałe - zapisuje się w postaci ciągów liter i cyfr rozpoczynających się od małej litery.
Przykłady termów złożonych:
W obu powyższych przykład para jest funktorem łączącym dwa termy w jeden.
W pierwszym przykładzie dwa proste termy a i b zostały połączone w jeden term para(a, b).
W drugim przykładzie prosty term a został połączony z termem złożonym para(b, c) w jeden term para(a, para(b, c)).
Termy proste to stałe i zmienne.
Termy złożone buduje się łącząc pewną liczbę termów w jeden.
Do łączenia służą funktory, które - podobnie jak stałe - zapisuje się w postaci ciągów liter i cyfr rozpoczynających się od małej litery.
Przykłady termów złożonych:
- para(a, b)
- para(a, para(b, c))
W obu powyższych przykład para jest funktorem łączącym dwa termy w jeden.
W pierwszym przykładzie dwa proste termy a i b zostały połączone w jeden term para(a, b).
W drugim przykładzie prosty term a został połączony z termem złożonym para(b, c) w jeden term para(a, para(b, c)).
Unifikacja
Podstawową operacją wykonywaną na termach jest ich unifikacja.
Rozstrzyga ona czy dwa termy mogą być identyczne.
Jeśli w unifikowanych termach występują zmienne, to celem zunifikowania termów konieczne może być podstawienie za zmienne pewnych termów.
Unifikację termów S i T zapisuje się w Prologu w postaci warunku S = T.
Przykłady:
W pierwszym przypadku unifikacja nie zachodzi bo stałe a i b są różne.
W drugim przypadku unifikacja zachodzi a przy okazji pod zmienną X zostaje podstawiona stała a.
W trzecim przypadku unifikacja zachodzi a pod zmienne X i Y zostają odpowiednio podstawione stałe a i b.
W czwartym przypadku unifikacja nie zachodzi bo pierwszy term jest parą dwóch różnych stałych a drugi term może być identyczny tylko z parami, których oba elementy są jednakowe.
Unifikację S = T, termów S i T, można rozumieć jako rozwiązywanie równania na wyrażeniach. W wyniku takiego rozwiązywania, jeśli istnieje rozwiązania równania, to za zmienne występujące w termach S i T zostają podstawione odpowiednie wartości (termy).
Rozstrzyga ona czy dwa termy mogą być identyczne.
Jeśli w unifikowanych termach występują zmienne, to celem zunifikowania termów konieczne może być podstawienie za zmienne pewnych termów.
Unifikację termów S i T zapisuje się w Prologu w postaci warunku S = T.
Przykłady:
- a = b
- a = X
- para(a, b) = para(X, Y)
- para(a, b) = para(X, X)
W pierwszym przypadku unifikacja nie zachodzi bo stałe a i b są różne.
W drugim przypadku unifikacja zachodzi a przy okazji pod zmienną X zostaje podstawiona stała a.
W trzecim przypadku unifikacja zachodzi a pod zmienne X i Y zostają odpowiednio podstawione stałe a i b.
W czwartym przypadku unifikacja nie zachodzi bo pierwszy term jest parą dwóch różnych stałych a drugi term może być identyczny tylko z parami, których oba elementy są jednakowe.
Unifikację S = T, termów S i T, można rozumieć jako rozwiązywanie równania na wyrażeniach. W wyniku takiego rozwiązywania, jeśli istnieje rozwiązania równania, to za zmienne występujące w termach S i T zostają podstawione odpowiednie wartości (termy).
Predykaty
W Prologu korzysta się z predykatów wyrażających warunki.
Wiele warunków jest zdefiniowanych w systemie Prolog i są one gotowe do wykorzystania zaraz po uruchomieniu systemu.
Jednym z dostępnych warunków jest unifikacja S = T.
Kolejnymi dostępnymi w Prologu predykatami są:
Mają one jeden argument i wyrażają następujące warunki:
Wiele warunków jest zdefiniowanych w systemie Prolog i są one gotowe do wykorzystania zaraz po uruchomieniu systemu.
Jednym z dostępnych warunków jest unifikacja S = T.
Kolejnymi dostępnymi w Prologu predykatami są:
- var(T)
- nonvar(T)
- atom(T)
- number(T)
- compound(T)
Mają one jeden argument i wyrażają następujące warunki:
- var(T) jest spełniony, gdy term T jest zmienną;
- nonvar(T) jest spełniony, gdy term T nie jest zmienną;
- atom(T) jest spełniony, gdy term T jest stałą ale nie liczbą;
- number(T) jest spełniony, gdy term T jest liczbą;
- compound(T) jest spełniony, gdy term T jest złożony.
Zadawanie pytań
Po uruchomieniu systemu Prolog pojawia się prompt będący zachętą do wpisania pytania.
W większości implementacji Prologu prompt ma postać dwóch znaków ?-.
Każde wpisane pytanie musi być zakończone kropką, po której naciskamy klawisz Enter celem wysłania go do systemu Prolog.
Najprostsze pytania składają się z pojedynczego warunku.
Przykładowy dialog z systemem SWI-Prolog:
?- number(10).
true.
?- atom(10).
false.
?- para(a, b) = para(X, Y).
X = a,
Y = b.
?- para(a, b) = para(X, X).
false.
Pytania mogą również mieć postać bardziej złożonych warunków.
Koniunkcję warunków zapisuje się łącząc je przecinkiem.
Oto przykładowy dialog, w wyniku którego pod zmienną Z zostaje podstawiona para dwóch termów w odwrotnej kolejności niż w pierwszym termie para(a, b):
?- para(a, b) = para(X, Y), Z = para(Y, X).
X = a,
Y = b,
Z = para(b, a).
Pierwsza unifikacja w powyższym przykładzie służy wydzieleniu w parze(a, b) pierwszego i drugiego jej elementu i podstawienie ich pod zmienne odpowiednio X i Y.
Druga unifikacja łączy termy podstawione za Y i X w nową parę i podstawia ją pod zmienną Z.
Warunki w pytaniu można również łączyć średnikiem oznaczającym spójnik alternatywy.
W takim przypadku system może znaleźć więcej niż jedną odpowiedź:
?- X = a; X = b.
X = a ;
X = b.
Po znalezieniu pierwszej odpowiedzi X = a można nacisnąć średnik a wówczas system Prolog znajdzie drugą odpowiedź X = b.
Warunki można również negować za pomocą operatora \+ (odwrócony ukośnik i plus).
Oto przykład dialogu, który dostarcza odpowiedzi na pytanie, który z dwóch elementów pary nie jest liczbą:
?- P = para(123, a), (P = para(E, _); P = para(_, E)), \+ number(E).
P = para(123, a),
E = a.
Powyższe zapytanie jest koniunkcją trzech warunków:
W większości implementacji Prologu prompt ma postać dwóch znaków ?-.
Każde wpisane pytanie musi być zakończone kropką, po której naciskamy klawisz Enter celem wysłania go do systemu Prolog.
Najprostsze pytania składają się z pojedynczego warunku.
Przykładowy dialog z systemem SWI-Prolog:
?- number(10).
true.
?- atom(10).
false.
?- para(a, b) = para(X, Y).
X = a,
Y = b.
?- para(a, b) = para(X, X).
false.
Pytania mogą również mieć postać bardziej złożonych warunków.
Koniunkcję warunków zapisuje się łącząc je przecinkiem.
Oto przykładowy dialog, w wyniku którego pod zmienną Z zostaje podstawiona para dwóch termów w odwrotnej kolejności niż w pierwszym termie para(a, b):
?- para(a, b) = para(X, Y), Z = para(Y, X).
X = a,
Y = b,
Z = para(b, a).
Pierwsza unifikacja w powyższym przykładzie służy wydzieleniu w parze(a, b) pierwszego i drugiego jej elementu i podstawienie ich pod zmienne odpowiednio X i Y.
Druga unifikacja łączy termy podstawione za Y i X w nową parę i podstawia ją pod zmienną Z.
Warunki w pytaniu można również łączyć średnikiem oznaczającym spójnik alternatywy.
W takim przypadku system może znaleźć więcej niż jedną odpowiedź:
?- X = a; X = b.
X = a ;
X = b.
Po znalezieniu pierwszej odpowiedzi X = a można nacisnąć średnik a wówczas system Prolog znajdzie drugą odpowiedź X = b.
Warunki można również negować za pomocą operatora \+ (odwrócony ukośnik i plus).
Oto przykład dialogu, który dostarcza odpowiedzi na pytanie, który z dwóch elementów pary nie jest liczbą:
?- P = para(123, a), (P = para(E, _); P = para(_, E)), \+ number(E).
P = para(123, a),
E = a.
Powyższe zapytanie jest koniunkcją trzech warunków:
- pierwszy warunek podstawia za zmienną P term para(123, a);
- drugi warunek jest alternatywą ustalającą zmienną E jako pierwszy albo drugi element pary P;
- trzeci warunek jest negacją predykatu sprawdzającego czy wartość zmiennej E jest liczbą.
Definiowanie predykatów
Programowanie w Prologu polega na definiowaniu predykatów.
Predykaty zapisuje się w postaci klauzul czyli zdań, przy czym każda klauzula musi być zakończona kropką.
Klauzule definiujące predykaty mogą być jednej z dwóch postaci:
Najprostszym przykładem faktów są klauzule definiujące predykat wyrażający trójczłonową relację między ojcem, matką i ich dzieckiem:
rodzice(uranus, gaia, rhea).
rodzice(uranus, gaia, cronus).
rodzice(cronus, rhea, zeus).
rodzice(cronus, rhea, hera).
rodzice(cronus, rhea, demeter).
rodzice(zeus, leto, artemis).
rodzice(zeus, leto, apollo).
rodzice(zeus, demeter, persephone).
Relację między ojcem i dzieckiem oraz między matką i dzieckiem można zapisać w postaci reguł:
ojciec(X, Y) :- rodzice(X, _, Y).
matka(X, Y) :- rodzice(_, X, Y).
W powyższych regułach symbol :- czytamy jako “jeśli” i oznacza wynikanie warunku po lewej jego stronie z warunku po stronie prawej.
Zatem reguły te możemy przeczytać następująco:
Relację bycia rodzicem możemy zdefiniować następująco:
rodzic(X, Y) :- ojciec(X, Y).
rodzic(X, Y) :- matka(X, Y).
Ten sam predykat dwuargumentowy rodzic możemy zapisać za pomocą jednej klauzuli używając spójnika alternatywy:
rodzic(X, Y) :- ojciec(X, Y); matka(X, Y).
ale osobiście odradzam takie skracanie zapisu (łatwiej zrozumieć zbiór prostszych reguł).
Poniższy dialog pokazuje jak znajdować rodzica dla danego dziecka i jak znajdować dzieci danego rodzica:
?- rodzic(Rodzic, zeus).
Rodzic = cronus ;
Rodzic = rhea ;
false.
?- rodzic(cronus, Dziecko).
Dziecko = zeus ;
Dziecko = hera ;
Dziecko = demeter ;
false.
Relacje bycia dziadkiem i bycia babcią można wyrazić następującymi klauzulami:
dziadek(X, Z) :- ojciec(X, Y), rodzic(Y, Z).
babcia(X, Z) :- matka(X, Y), rodzic(Y, Z).
Powyższe klauzule możemy odczytać następująco:
Zależności między ojcem, rodzicem i dziadkiem możemy przedstawić jak na poniższym diagramie:
Predykaty zapisuje się w postaci klauzul czyli zdań, przy czym każda klauzula musi być zakończona kropką.
Klauzule definiujące predykaty mogą być jednej z dwóch postaci:
- fakty;
- reguły.
Najprostszym przykładem faktów są klauzule definiujące predykat wyrażający trójczłonową relację między ojcem, matką i ich dzieckiem:
rodzice(uranus, gaia, rhea).
rodzice(uranus, gaia, cronus).
rodzice(cronus, rhea, zeus).
rodzice(cronus, rhea, hera).
rodzice(cronus, rhea, demeter).
rodzice(zeus, leto, artemis).
rodzice(zeus, leto, apollo).
rodzice(zeus, demeter, persephone).
Relację między ojcem i dzieckiem oraz między matką i dzieckiem można zapisać w postaci reguł:
ojciec(X, Y) :- rodzice(X, _, Y).
matka(X, Y) :- rodzice(_, X, Y).
W powyższych regułach symbol :- czytamy jako “jeśli” i oznacza wynikanie warunku po lewej jego stronie z warunku po stronie prawej.
Zatem reguły te możemy przeczytać następująco:
- jeśli X jest pierwszym rodzicem dla Y, to X jest ojcem Y;
- jeśli X jest drugim rodzicem dla Y, to X jest matką Y.
Relację bycia rodzicem możemy zdefiniować następująco:
rodzic(X, Y) :- ojciec(X, Y).
rodzic(X, Y) :- matka(X, Y).
Ten sam predykat dwuargumentowy rodzic możemy zapisać za pomocą jednej klauzuli używając spójnika alternatywy:
rodzic(X, Y) :- ojciec(X, Y); matka(X, Y).
ale osobiście odradzam takie skracanie zapisu (łatwiej zrozumieć zbiór prostszych reguł).
Poniższy dialog pokazuje jak znajdować rodzica dla danego dziecka i jak znajdować dzieci danego rodzica:
?- rodzic(Rodzic, zeus).
Rodzic = cronus ;
Rodzic = rhea ;
false.
?- rodzic(cronus, Dziecko).
Dziecko = zeus ;
Dziecko = hera ;
Dziecko = demeter ;
false.
Relacje bycia dziadkiem i bycia babcią można wyrazić następującymi klauzulami:
dziadek(X, Z) :- ojciec(X, Y), rodzic(Y, Z).
babcia(X, Z) :- matka(X, Y), rodzic(Y, Z).
Powyższe klauzule możemy odczytać następująco:
- jeśli X jest ojcem Y i Y jest rodzicem Z, to X jest dziadkiem Z;
- jeśli X jest matką Y i Y jest rodzicem Z, to X jest babcią Z.
Zależności między ojcem, rodzicem i dziadkiem możemy przedstawić jak na poniższym diagramie:
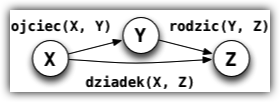
I jeszcze dialog, w którym poszukujemy dziadka jakiego miała Persefona:
?- dziadek(Dziadek, persephone).
Dziadek = cronus ;
Dziadek = cronus ;
false.
Dwie takie same odpowiedzi (dwa razy Kronos) wynikają z tego, że Persefona była córką rodzeństwa (Zeusa i Demeter) więc Kronos jest ojcem zarówno ojca jak i matki Persefony.
W powyższych przykładach korzystaliśmy z prostych stałych reprezentujących postacie z mitologii greckiej.
W kolejnych przykładach pokażemy jak wyrażać relacje (warunki) między złożonymi danymi reprezentowanymi złożonymi termami.
Rozpoczniemy od warunku stwierdzającego co jest elementem pary (pierwszym lub drugim):
element(X, para(X, _)).
element(X, para(_, X)).
W poniższym dialogu znajdowany jest element E2 będący elementem elementu E pary P:
?- P = para(a, para(b, c)), element(E, P), element(E2, E).
P = para(a, para(b, c)),
E = para(b, c),
E2 = b ;
P = para(a, para(b, c)),
E = para(b, c),
E2 = c.
Pary mogą składać się z dowolnie zagnieżdżonych innych par, więc przydać się może relacja wystepuje_w, która jest przechodnim domknięciem relacji bycia elementem (coś występuje w parze jeśli jest jej elementem albo występuje w elemencie pary):
wystepuje_w(X, Y) :- element(X, Y).
wystepuje_w(X, Z) :- element(Y, Z), wystepuje_w(X, Y).
Poniższy przykład pokazuje znajdowanie wszystkich elementów E występujących w parze P:
?- P = para(a, para(b, c)), wystepuje_w(E, P).
P = para(a, para(b, c)),
E = a ;
P = para(a, para(b, c)),
E = para(b, c) ;
P = para(a, para(b, c)),
E = b ;
P = para(a, para(b, c)),
E = c ;
false.
?- dziadek(Dziadek, persephone).
Dziadek = cronus ;
Dziadek = cronus ;
false.
Dwie takie same odpowiedzi (dwa razy Kronos) wynikają z tego, że Persefona była córką rodzeństwa (Zeusa i Demeter) więc Kronos jest ojcem zarówno ojca jak i matki Persefony.
W powyższych przykładach korzystaliśmy z prostych stałych reprezentujących postacie z mitologii greckiej.
W kolejnych przykładach pokażemy jak wyrażać relacje (warunki) między złożonymi danymi reprezentowanymi złożonymi termami.
Rozpoczniemy od warunku stwierdzającego co jest elementem pary (pierwszym lub drugim):
element(X, para(X, _)).
element(X, para(_, X)).
W poniższym dialogu znajdowany jest element E2 będący elementem elementu E pary P:
?- P = para(a, para(b, c)), element(E, P), element(E2, E).
P = para(a, para(b, c)),
E = para(b, c),
E2 = b ;
P = para(a, para(b, c)),
E = para(b, c),
E2 = c.
Pary mogą składać się z dowolnie zagnieżdżonych innych par, więc przydać się może relacja wystepuje_w, która jest przechodnim domknięciem relacji bycia elementem (coś występuje w parze jeśli jest jej elementem albo występuje w elemencie pary):
wystepuje_w(X, Y) :- element(X, Y).
wystepuje_w(X, Z) :- element(Y, Z), wystepuje_w(X, Y).
Poniższy przykład pokazuje znajdowanie wszystkich elementów E występujących w parze P:
?- P = para(a, para(b, c)), wystepuje_w(E, P).
P = para(a, para(b, c)),
E = a ;
P = para(a, para(b, c)),
E = para(b, c) ;
P = para(a, para(b, c)),
E = b ;
P = para(a, para(b, c)),
E = c ;
false.
Listy i warunki na listach
Szczególnym przykładem termów złożonych są listy.
Powstają one jako połączenie pierwszego elementu listy (głowa listy) z listą pozostałych elementów (ogon listy).
Funktor łączący głowę z ogonem listy nazywa się w Prologu . (kropka), natomiast stała oznaczająca listę pustą nazywa się [] (kwadratowy nawias otwierający i zamykający).
Przykłady list:
Jak widać zapis ten jest mało czytelny dla człowieka. Dlatego w Prologu korzysta się z drugiej notacji list, w której kolejne elementy listy umieszcza się między nawiasami kwadratowymi i oddziela przecinkami.
Listy z powyższego przykładu zapisać możemy następująco:
W tej czytelnej dla człowieka notacji od razu widać, że czwarta lista z powyższego wykazu składa się z dwóch elementów, przy czym pierwszym jej elementem jest lista jednoelementowa a drugim lista dwuelementowa.
Poniższy dialog pokazuje równoważność obu notacji list:
?- [[a], [a, b]] = .(.(a, []), .(.(a, .(b, [])), [])).
true.
?- [[a], [a, b]] = .(X, .(Y, Z)).
X = [a],
Y = [a, b],
Z = [].
?- [[a], [a, b]] = .(_, .(X, _)).
X = [a, b].
W ostatnim pytaniu powyższego przykładu pytamy się o drugi element listy. W tym celu unifikujemy listę z termem .(_, .(X, _)) będącym wzorcem pasującym do list co najmniej dwuelementowych o drugim elemencie X.
Aby zapisać podobny wzorzec w notacji z nawiasami kwadratowymi potrzebny jest operator | (pionowa kreska) oddzielający początkowe elementy listy od listy pozostałych elementów:
?- [[a], [a, b]] = [_, X | _].
X = [a, b].
W przeciwieństwie do języków algorytmicznych (imperatywnych, proceduralnych) jak np. C nie jest konieczne w Prologu deklarowanie struktur i samodzielne rezerwowanie i zwalnianie dla nich pamięci. Struktury takie jak listy są w Prologu po prostu wyrażeniami, które mogą występować w równaniach (unifikacji) i dzięki temu mogą być składane i rozkładane.
Oto przykład dialogu, w którym pod listę L2 podstawia się lista będąca odwróceniem listy L1:
?- L1 = [1, 2, 3, 4], L1 = [A, B, C, D], L2 = [D, C, B, A].
L1 = [1, 2, 3, 4],
A = 1,
B = 2,
C = 3,
D = 4,
L2 = [4, 3, 2, 1].
W Prologu dostępnych jest wiele predykatów wyrażających warunki na listach.
Najważniejsze z nich to:
Należy zwrócić uwagę, że powyższe warunki mogą być spełnione na wiele sposobów dostarczając wiele odpowiedzi.
Na przykład, jeśli pytamy się o element listy trójelementowej, to otrzymamy trzy odpowiedzi:
?- member(X, [a, b, c]).
X = a ;
X = b ;
X = c.
Co więcej, Prolog wyraża relacje a nie tylko funkcje, więc predykat append można używać nie tylko do składania list ale również do ich rozrywania:
?- append([1, 2], [3, 4, 5], X).
X = [1, 2, 3, 4, 5].
?- append(X, Y, [a, b, c]).
X = [],
Y = [a, b, c] ;
X = [a],
Y = [b, c] ;
X = [a, b],
Y = [c] ;
X = [a, b, c],
Y = [] ;
false.
Podobnie predykat select może wyjmować elementy z listy ale i wkładać je do listy:
?- select(X, [1, 2, 3], L).
X = 1,
L = [2, 3] ;
X = 2,
L = [1, 3] ;
X = 3,
L = [1, 2] ;
false.
?- select(a, L, [1, 2]).
L = [a, 1, 2] ;
L = [1, a, 2] ;
L = [1, 2, a] ;
false.
Taką uniwersalność predykatów Prolog zawdzięcza temu, że programy w nim opisują CO to znaczy być elementem albo połączeniem list a nie JAK wyjąć element albo połączyć listy.
Nie powinno więc dziwić, że definicje takich uniwersalnych predykatów są w Prologu krótkie i proste do zrozumienia:
member(X, [X | _]).
member(X, [_ | Y]) :- member(X, Y).
append([], X, X).
append([X | Y1], Y2, [X | Z]) :- append(Y1, Y2, Z).
select(X, [X | Y], Y).
select(X, [Y | Z1], [Y | Z2]) :- select(X, Z1, Z2).
Powyższe klauzule są formalnie zapisanymi definicjami jakie możemy wyrazić następująco w języku polskim:
Powstają one jako połączenie pierwszego elementu listy (głowa listy) z listą pozostałych elementów (ogon listy).
Funktor łączący głowę z ogonem listy nazywa się w Prologu . (kropka), natomiast stała oznaczająca listę pustą nazywa się [] (kwadratowy nawias otwierający i zamykający).
Przykłady list:
- []
- .(a, [])
- .(a, .(b, []))
- .(.(a, []), .(.(a, .(b, [])), []))
Jak widać zapis ten jest mało czytelny dla człowieka. Dlatego w Prologu korzysta się z drugiej notacji list, w której kolejne elementy listy umieszcza się między nawiasami kwadratowymi i oddziela przecinkami.
Listy z powyższego przykładu zapisać możemy następująco:
- []
- [a]
- [a, b]
- [[a], [a, b]]
W tej czytelnej dla człowieka notacji od razu widać, że czwarta lista z powyższego wykazu składa się z dwóch elementów, przy czym pierwszym jej elementem jest lista jednoelementowa a drugim lista dwuelementowa.
Poniższy dialog pokazuje równoważność obu notacji list:
?- [[a], [a, b]] = .(.(a, []), .(.(a, .(b, [])), [])).
true.
?- [[a], [a, b]] = .(X, .(Y, Z)).
X = [a],
Y = [a, b],
Z = [].
?- [[a], [a, b]] = .(_, .(X, _)).
X = [a, b].
W ostatnim pytaniu powyższego przykładu pytamy się o drugi element listy. W tym celu unifikujemy listę z termem .(_, .(X, _)) będącym wzorcem pasującym do list co najmniej dwuelementowych o drugim elemencie X.
Aby zapisać podobny wzorzec w notacji z nawiasami kwadratowymi potrzebny jest operator | (pionowa kreska) oddzielający początkowe elementy listy od listy pozostałych elementów:
?- [[a], [a, b]] = [_, X | _].
X = [a, b].
W przeciwieństwie do języków algorytmicznych (imperatywnych, proceduralnych) jak np. C nie jest konieczne w Prologu deklarowanie struktur i samodzielne rezerwowanie i zwalnianie dla nich pamięci. Struktury takie jak listy są w Prologu po prostu wyrażeniami, które mogą występować w równaniach (unifikacji) i dzięki temu mogą być składane i rozkładane.
Oto przykład dialogu, w którym pod listę L2 podstawia się lista będąca odwróceniem listy L1:
?- L1 = [1, 2, 3, 4], L1 = [A, B, C, D], L2 = [D, C, B, A].
L1 = [1, 2, 3, 4],
A = 1,
B = 2,
C = 3,
D = 4,
L2 = [4, 3, 2, 1].
W Prologu dostępnych jest wiele predykatów wyrażających warunki na listach.
Najważniejsze z nich to:
- member(X, L) spełniony, gdy X jest elementem listy L;
- append(L1, L2, L3) spełniony, gdy lista L3 jest połączeniem list L1 i L2;
- select(X, L1, L2) spełniony, gdy lista L2 jest listą pozostałą z listy L1 po wyjęciu z niej elementu X.
Należy zwrócić uwagę, że powyższe warunki mogą być spełnione na wiele sposobów dostarczając wiele odpowiedzi.
Na przykład, jeśli pytamy się o element listy trójelementowej, to otrzymamy trzy odpowiedzi:
?- member(X, [a, b, c]).
X = a ;
X = b ;
X = c.
Co więcej, Prolog wyraża relacje a nie tylko funkcje, więc predykat append można używać nie tylko do składania list ale również do ich rozrywania:
?- append([1, 2], [3, 4, 5], X).
X = [1, 2, 3, 4, 5].
?- append(X, Y, [a, b, c]).
X = [],
Y = [a, b, c] ;
X = [a],
Y = [b, c] ;
X = [a, b],
Y = [c] ;
X = [a, b, c],
Y = [] ;
false.
Podobnie predykat select może wyjmować elementy z listy ale i wkładać je do listy:
?- select(X, [1, 2, 3], L).
X = 1,
L = [2, 3] ;
X = 2,
L = [1, 3] ;
X = 3,
L = [1, 2] ;
false.
?- select(a, L, [1, 2]).
L = [a, 1, 2] ;
L = [1, a, 2] ;
L = [1, 2, a] ;
false.
Taką uniwersalność predykatów Prolog zawdzięcza temu, że programy w nim opisują CO to znaczy być elementem albo połączeniem list a nie JAK wyjąć element albo połączyć listy.
Nie powinno więc dziwić, że definicje takich uniwersalnych predykatów są w Prologu krótkie i proste do zrozumienia:
member(X, [X | _]).
member(X, [_ | Y]) :- member(X, Y).
append([], X, X).
append([X | Y1], Y2, [X | Z]) :- append(Y1, Y2, Z).
select(X, [X | Y], Y).
select(X, [Y | Z1], [Y | Z2]) :- select(X, Z1, Z2).
Powyższe klauzule są formalnie zapisanymi definicjami jakie możemy wyrazić następująco w języku polskim:
- X jest elementem listy o głowie X oraz jeśli X jest elementem listy Y, to X jest elementem listy o ogonie Y;
- połączeniem listy pustej z dowolną listą X jest lista X oraz jeśli Z jest połączeniem list Y1 i Y2, to lista o głowie X i ogonie Z jest połączeniem listy o głowie X i ogonie Y1 z listą Y2;
- po wyjęciu elementu z listy o głowie X i ogonie Y pozostaje lista Y oraz jeśli lista Z2 powstaje z listy Z1 przez wyjęcie elementu X, to lista o głowie Y i ogonie Z2 powstaje z listy o głowie Y i ogonie Z1 przez wyjęcie z niej elementu X.