• Data: 29.02.2016
• Wykładowca: prof. dr hab. Jacek Cichoń

Twierdzenie Pitagorasa

• Dowód układankowy: aplet (poczekaj chwilę, aż zacznie się animacja na tym aplecie)
• Dowód algebraiczny:
  
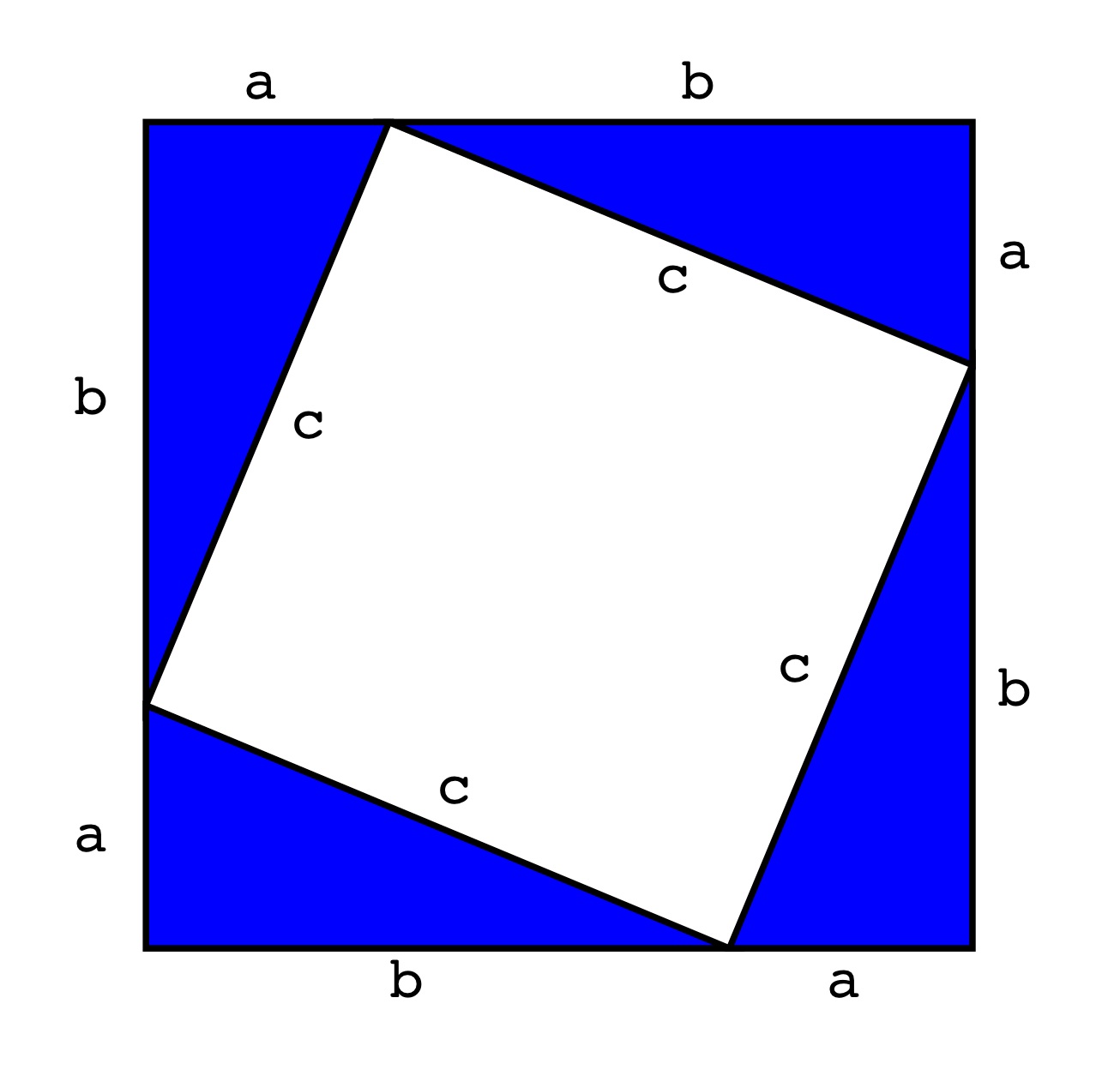
  1. Pole dużego kwadratu: $P = (a+b)^2$
  2. Pole liczone inaczej: $P$ = cztery trójąty o powierzchni $\frac12 \cdot a \cdot b$ + kwadrat o polu $c^2$
  3. Zatem $(a+b)^2 = 4 \cdot \frac12 \cdot a \cdot b + c^2$
  4. Zatem $a^2+ 2\cdot a\cdot b + b^2 = 2 \cdot a \cdot b + c^2$
  5. Zatem $a^2 + b^2 = c^2$
• Kilka wniosków:
  1. Długość przekątnej kwadratu o boku 1: $\sqrt{2}$
  2. Długość przekątnej sześcianu o boku 1: $\sqrt{3}$

Na kolejnym spotkaniu, udowodnimy twierdzenie odwrotne do twierdzenia Pitagorasa.

Zadania

1. Jaka jest długość przekątnej prostokąta o bokach długości $a$ i $b$?
2. Jaka jest dlugość najdłuższej przekątnej prostopadłościanu o bokach długości $a$, $b$ i $c$?

• Data: 18.04.2016
• Wykładowca: prof. dr hab. Jacek Cichoń

Trójki Pitagorejskie

• Odwrotne Twierdzenie Pitagorasa: jeśli trójąt ma boki długości a, b, c oraz $a^2+b^2 = c^2$, to kąt przy wierzchołku leżącym naprzeciw boku o długości c jest kątem prostym.
• Przykład: trójkąt o bokach o dlugości 3, 4, 5 jest trójkątem prostokątnym !!!
• Pokazaliśmy jak ze sznurka można zbudować trójkąt prostokątny
• Wspólnie pokazaliśmy, że
  1. $(n^2 - m^2)^2 = n^4 - 2 n^2 m^2 + m^4$
  2. $(n^2 + m^2)^2 = n^4 + 2 n^2 m^2 + m^4$
  i z tego wypólnie wywnioskowaliśmy, że $$ (n^2 - m^2)^2 + (2nm)^2 = (n^2 + m^2)^2 $$ Po podstawieniu do tego wzorku liczb n=2, m=1 otrzymaliśmy trójkąt o bokach o długości 3, 4 i 5.
  Podtawienie n=3 i m=1 nie dało nic ciekawego: otrzymaliśmy trójkąt o bokach o długości 6, 8 i 10.
  Ale podstawienie n=4, m=1 dało nam nową trojkę Pitagorejską: 8, 15, 17.

Zadania

1. Weź sznurek długości 3.6 m. Zwiąż końce. Zaznacz na nim punkty leżące w odległości 90 cm oraz 120 cm od miejsca połączenia. Rozciągnuj boki tak, aby zbudować trójkąt prostokątny.
2. Zastosuj wyprowadzony wzorek dla n=3 i m=2. Sprawdź, że otrzymamy trójkąt Pitagorejski.
3. Zastosuj wyprowadzony wzorek dla n=4 i m=1. Sprawdź, że otrzymamy trójkąt Pitagorejski.
4. Zastosuj wyprowadzony wzorek dla n=4 i m=3. Sprawdź, że otrzymamy trójkąt Pitagorejski.

• Data: 14.03.2016
• Wykładowca: dr Szymon Żeberski

Funkcje

• Zbiór $R$ nazywamy relacją jeśli $R\subseteq X\times X$, dla pewnego zbioru $X$.
• Niech $R,\ S$ będą relacjami. Wtedy:
• $R\circ S=\{(x,y):\ (\exists z)(x,z)\in S\land (z,y)\in R)\}$,
• $R^{-1}=\{(x,y):\ (y,x)\in R\}$.
• Zbiór $f$ nazywamy funkcją jeśli $f$ jest relacją oraz $$(\forall x,y_1,y_2)((x,y_1)\in f\land (x,y_2)\in f\rightarrow y_1=y_2)$$
• Zamiast $(x,y)\in f$ piszemy $y=f(x).$
• Złożenie funkcji jest funkcją. $f\circ g (x)= f(g(x))$.
• Relacja odwrotna do funkcji nie musi być funkcją!
• Niech $R$ będzie relacją. Wtedy:
• Dziedziną relacji $R$ nazywamy zbiór $dom(R)=\{x:\ (\exists y)( (x,y)\in R)\}$,
• Obrazem relacji $R$ nazywamy zbiór $rng(R)=\{y:\ (\exists x)( (x,y)\in R)\}$.
• Piszemy $f:A\to B$ jeśli $f$ jest funkcją, $dom(f)=A$ oraz $rng(f)\subseteq B$.
• $B^A=\{f:\ f:A\to B\}$.
• $X^\emptyset=\{\emptyset\}$.
• Obcięciem funkcji $f$ do zbioru $A$ nazywamy zbiór $f| A=f\cap(A\times rng(f))$.
• Obcięcie funkcji jest funkcją.

Zadania

1. Niech $f,g$ będą funkcjami. Udowodnij, że $f\cap g$, $f\setminus g$ są funkcjami. Czy $f\cup g$ jest funkcją?
2. Niech $f$ będzie funkcją. Czy $f\circ f^{-1}$ jest funkcją? Czy $f^{-1}\circ f$ jest funkcją?
3. Wyznacz $\emptyset^X$ dla dowolnego niepustego zbioru $X$.
4. Udowodnij, że jeśli $f$ jest funkcją, to $f| A$ jest funkcją oraz $dom(f| A)=dom(f)\cap A$.

• Data: 21.03.2016
• Wykładowca: dr Krzysztof Majcher

Funkcje różnowartościowe i "na"

• Niech $f:A \rightarrow B$ będzie funkcją. Wtedy
• $f$ nazywamy różnowartościową (iniekcją) wtedy i tylko wtedy, gdy dla dowolnych $x,y \in A$ jeżeli $x \neq y$, to $f(x) \neq f(y)$.
• $f$ nazywamy "na" (suriekcją) wtedy i tylko wtedy, gdy dla dowolnego $y \in B$ istnieje taki $x \in A$, że $f(x)=y$.
• $f$ nazywamy bijekcją wtedy i tylko wtedy, gdy $f$ jest różnowartościową suriekcją.
• Twierdzenie. Niech $f:A \rightarrow B$ oraz $g:B \rightarrow C$. Wtedy
• jeśli funkcje $f,\ g$ są różnowartościowe, to ich złożenie $g \circ f: A \rightarrow C$ jest funkcją różnowartościową,
• jeśli funkcje $f,\ g$ są surjekcjami, to ich złożenie $g \circ f: A \rightarrow C$ jest surjekcją.
• Twierdzenie. Jeśli funkcja $f:A \rightarrow B$ jest bijekcją, to istnieje dokładnie jedna funkcja $g:B \rightarrow A$ taka, że złożenie $g \circ f: A \rightarrow A$ jest identycznością na $A$.
• Funkcję $g$ nazywamy funkcją odwrotną do funkcji $f$ i oznaczamy $f^{-1}$.
• Przykłady
• Jeśli zbiór $Z$ ma $n \in \mathbb{N}$ elementów, to istnieje bijekcja ze zbioru $Z$ w zbiór $\{1,2,...,n\}$.
• Funkcja $f(x)=2x$ jest bijekcją ze zbioru liczb naturalnych w liczby parzyste.

Zadania

1. Pokaż, że dla dowolnych liczb rzeczywistych $a,\ b\in\mathbb{R}$, jeśli $a\neq 0$, to funkcja $f:\mathbb{R} \rightarrow \mathbb{R}$ zadana wzorem $f(x)=ax+b$ jest bijekcją.
2. Ile jest bijekcji $f: \{1,2,...,n \} \rightarrow \{1,2,...,n \}$?
3. Czy istnieje skończony zbiór $A$ oraz różnowartościowa funkcja $f:A \rightarrow A$, która nie jest surjekcją?
4. Napisz wzorem bijekcję ze zbioru liczb parzystych w zbiór liczb podzielnych przez trzy.

• Data: 25.04.2016
• Wykładowca: dr hab. Szymon Żeberski

Pojęcie równoliczności

• Mówimy, że zbiory $A$, $B$ są równoliczne wtedy i tylko wtedy, gdy istnieje bijekcja $f:A \rightarrow B$. Piszemy wówczas $|A|=|B|$.
• Przykłady
• $|\mathbb{N}|=|\mathbb{Z}|$,
• $|(0,1)|=|(2,17)|$ (świadczy o tym funkcja $f(x)=2+15x$),
• dowolne dwa otwarte odcinki są równoliczne,
• $|(-\frac{\pi}{2},\frac{\pi}{2})|=|\mathbb{R}|$ (świadczy o tym funkcja $f(x)=tg(x)$).
• Niech $A,\ B$ będą zbiorami. Piszemy
• $|A|\le |B|$ wtedy i tylko wtedy, gdy istnieje iniekcja $f:A\to B$,
• $|A|<|B|$ wtedy i tylko wtedy, gdy $|A|\le |B|$ oraz $|A|\neq |B|$.
• Twierdzenie Cantora-Bernsteina. Jeśli $|A|\le |B|$ oraz $|B|\le |A|$, to $|A|=|B|$.
• Twierdzenie Cantora. Dla dowolnego zbioru $A$ mamay $|A|<|P(A)|$.
• Wniosek. Istnieją różne nieskończoności!!

Zadania

1. Udowodnij, że zbiory $(0,1)\cup [2,3]$ oraz $[1,2]\cup (3,5)$ są równoliczne.
2. Pokaż, że odcinek otwarty $(0,1)$ jest równoliczny z odcinkiem domkniętym $[0,1]$.
3. Znajdź bijekcję pomiędzy zbiorem liczb niewymiernych i zbiorem wszystkich liczb rzeczywistych.
4. Udowodnij, że zbiór pierwiastków wszystkich trójmianów kwadratowych o współczynnikach wymiernych jest równoliczny ze zbiorem liczb naturalnych.
5. Udowodnij, że $|\mathbb{N}|<|\mathbb{N}^\mathbb{N}|$.

• Data: 06.06.2016
• Wykładowca: dr Robert Rałowski

Zbiory przeliczalne

• Definicja. Zbiór $A$ jest przeliczalny jeśli $A=\emptyset$ lub istnieje suriekcja $f:\mathbb{N}\to A$
• Twierdzenie. Zbiór $A$ jest przeliczalny wtedy i tylko wtedy, gdy jest skończony lub $|A|=\aleph_0$
• Twierdzenie. $|\mathbb{N}\times \mathbb{N}| = |\mathbb{N}| = \aleph_0$.
• Twierdzenie. $\mathbb{Z}$ oraz $\mathbb{Q}$ są przeliczalne.
• Twierdzenie. Jeśli $A$ i $B$ są przeliczalne, to $A\times B$ jest również przeliczalny.
• Twierdzenie. Jeśli $A_1,\ldots, A_n$ są przeliczalne, to $A\times\ldots\times A_n$ jest również przeliczalny.
• Twierdzenie (AC). Jeśli $\{ A_n:\; n\in\mathbb{N}\}$ jest przeliczalną rodziną zbiorów przeliczalnych, to suma mnogościowa $\bigcup_{n\in\mathbb{N}} A_n$ jest zbiorem przeliczalnym.
• Twierdzenie. Niech $K\subseteq \mathbb{R}$ będzie zbiorem przeliczalnym, to
  1. $(\forall n\in\mathbb{N})\; (K_n[x]=\{f\in K[x]: st(f) = n\}\text{ jest przeliczalny})$,
  2. $K[x]$ jest przeliczalny
  3. $\{ x\in \mathbb{R}:\; (\exists n\in\mathbb{N})(\exists f\in K_n[x])\; (f(x) = 0)\}$ jest przeliczalny.
• Definicja. Liczba rzeczywista $a\in\mathbb{R}$ jest algebraiczna wtedy i tylko wtedy, gdy istnieje taki niezerowy wielomian $f\in \mathbb{Q}[x]$, że $f(a) = 0$.
• Twierdzenie (Cantor). Zbiór wszystkich liczb algebraicznych jest przeliczalny. Istnieją niealgebraiczne (przestępne) liczby rzeczywiste.

Zadania

1. Udowodnij, że zbiór wszytkich odcinków o końcach wymiernych jest przeliczalny.
2. Udowodnij, że na płaszczyźnie $\mathbb{R}^2$, dowolna rodzina parami rozłącznych kół otwartych jest przeliczalna.
3. Udowodnij, że na płaszczyźnie $\mathbb{R}^2$ można zapisać tylko przeliczalnie wiele parami rozłącznych liter $T$ (górna kreska ma taką samą długość jak dolna kreska). Wskazówka, dla każdej dodatniej liczby naturalnej $n$, rozważ podrodzinę $\mathcal{R}_n$, której elementami są litery $T$ o długości kreski poziomej większej niż $\frac{1}{n}$.
4. Pokaż, że można wybrać przeliczalną rodzinę kół otwartych $\mathcal{R}$ na płaszczyźnie rzeczywistej $\mathbb{R}^2$ o tej własności, że każdy zbiór otwarty jest sumą pewnej podrodziny rodziny $\mathcal{R}$. Tutaj $A\subseteq \mathbb{R}^2$ jest zbiorem otwartym, jeśli spełniony jest warunek $$ (\forall x\in U)(\exists r>0)\; (K(x,r)\subseteq U). $$ $K(x,r)$ jest kołem otwartym w $\mathbb{R}^2$ o środku $x\in \mathbb{R}^2$ i promieniu $r>0$. Ponadto, jeśli $x=(x_1,x_2)\in \mathbb{R}^2$, to $$ K(x,r) = \big\{ (y_1,y_2) \in \mathbb{R}^2 :\; \sqrt{ (x_1-y_1)^2 + (x_2-y_2)^2 } < r \big\}. $$

• Data: 13.06.2016
• Wykładowca: dr hab. Szymon Żeberski

Zbiory mocy continuum

• Mówimy, że zbiór $A$ jest mocy continuum wtedy i tylko wtedy, gdy $|A|=|\mathbb{R}|$, czyli istnieje bijekcja $f:A \rightarrow \mathbb{R}$. Piszemy wówczas $|A|=\mathfrak c$.
• Twierdzenie. $|P(\mathbb{N})|=\mathfrak c$.
• Dowód opiera się na twierdzeniu Cantora-Bernsteina oraz $|P(\mathbb{N})|=|\{0,1\}^\mathbb{N}|=|P(\mathbb{Q})|$.
• Wniosek. $|\mathbb{N}|<|\mathbb{R}|$.
• Dowód używa twierdzenia Cantora.
• Przykłady zbiorów mocy continuum
• "trójkowy zbiór Cantora", który pojawia się w dowodzie twierdzenia (jest to zbiór liczb rzeczywistych z odcinka $[0,1]$, w zapisie trójkowym których występują wyłącznie cyrfy 0 lub 2),
• $\mathbb{R}\times\mathbb{R},\ \mathbb{R}^2,\ \mathbb{R}^n$,
• $\mathbb{R}^\mathbb{N}$, czyli zbiór ciągów rzeczywistych.

Zadania

1. Udowodnij, że suma długości odcinków, które "wyrzucamy" z odcinka $[0,1]$ konstruując "trójkowy zbiór Cantora" jest równa 1.
2. Udowodnij, że dowolny zbiór mocy continuum można podzielić na continuum zbiorów mocy continuum.
3. Opisz rozkład z poprzedniego zadania dla "trójkowego zbioru Cantora".
4. Udowodnij, że zbiór liczb przestępnych jest mocy continuum.

• Data: 19.10.2015
• Wykładowca: prof. dr hab. Jacek Cichoń

1. Dla dowolnego $n\geq 1$ przez $\mathbb{R}^n$ oznaczamy zbiór wszytkich "$n$-ek" liczb rzeczywistych, czyli $$ \mathbb{R}^n = \{(x_1,x_2,\ldots,x_n): x_1, x_2, \ldots, x_n \in \mathbb{R} \}~. $$ Niech $\vec{x}=(x_1,x_2,\ldots,x_n)$, $\vec{y}=(y_1,y_2,\ldots,y_n)$ będą wektorami z $\mathbb{R}^n$. Niech $\lambda \in \mathbb{R}$. Określamy:
   1. $\vec{x}+\vec{y} = (x_1+y_1,x_2+y_2, \ldots, x_n+y_n)$
   2. $\lambda \cdot \vec{x} = (\lambda \cdot x_1, \lambda \cdot x_2, \ldots, \lambda \cdot x_n)$
   Uwaga: wektory mnożymy przez liczby. Nie rozważamy mnożenia wektorów przez wektory.
   
2. Podstawowe własności:
   1. $\vec{x}+\vec{y} = \vec{y}+\vec{x}$
   2. $\lambda\cdot(\vec{x}+\vec{y}) = \lambda\cdot\vec{y}+\lambda\cdot\vec{x}$
3. Def. Długość wektora $\vec{x}\in\mathbb{R}^n$ określamy wzorem $|\!|\vec{x}|\!| = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}~.$
   
4. Dla $n=2$ oraz $n=3$ sprawdziliśmy, korzystajac z Twierdzenia Pitagorasa, że liczba $|\!|\vec{x}|\!|$ jest równa długości wektora $\vec{x}$.
5. Pokazaliśmy, że
   1. $|\!|\lambda \vec{x} |\!| = |\lambda| \cdot |\!|\vec{x}|\!|$.
   2. $\vec{x} + (\vec{y}-\vec{x}) = \vec{y}$.
   3. Odległość między "końcami" wektorów $\vec{x}$, $\vec{y}$ wyraża się wzorem $d(\vec{x},\vec{y}) = |\!|\vec{x} - \vec{y}|\!|$.
   4. Środek odcinka łączącego końce wektorów $\vec{a}$ oraz $\vec{b}$ ma współrzędne $\frac12(\vec{a}+\vec{b})$.

Lista zadań: ZSA_KI_LO_2015_W1.pdf.

Iloczyn skalarny i odległość w $\mathbb{R}^n$

• Data: 2.11.2015
• Wykładowca: dr Szymon Żeberski

1. Niech $\vec{x}=(x_1,x_2,\ldots,x_n)$, $\vec{y}=(y_1,y_2,\ldots,y_n)$ będą wektorami z $\mathbb{R}^n$.
   Iloczynem skalarnym wektorów $\vec{x},\ \vec{y}$ nazywamy liczbę $$ \langle\vec{x},\vec{y}\rangle=\sum_{i=1}^nx_iy_i=x_1y_1+x_2y_2+\cdots+x_ny_n $$
2. Własności iloczynu skalarnego:
   1. $\langle\vec{x}+\vec{y},\vec{z}\rangle=\langle\vec{x},\vec{z}\rangle+\langle\vec{y},\vec{z}\rangle$, $\langle\vec{x},\vec{y}+\vec{z}\rangle=\langle\vec{x},\vec{y}\rangle+\langle\vec{x},\vec{z}\rangle$,
   2. $\langle\lambda\vec{x},\vec{y}\rangle=\lambda\langle\vec{x},\vec{y}\rangle=\langle\vec{x},\lambda\vec{y}\rangle$,
   3. $\langle\vec{x},\vec{y}\rangle=\langle\vec{y},\vec{x}\rangle$,
   4. $\langle\vec{x},\vec{x}\rangle\ge 0$, równość zachodzi tylko dla $\vec{x}=(0,0,\ldots,0)$.
3. Def. Normą wektora $\vec{x}$ nazywamy nieujemną liczbę $|\!|\vec{x}|\!|=\sqrt{\langle\vec{x},\vec{x}\rangle}$.
4. Tw. (Nierówność Cauchy'ego-Schwarza) $$\left|\langle\vec{x},\vec{y}\rangle\right| \le |\!|\vec{x}|\!| \cdot |\!|\vec{y}|\!|$$ $$ \left|\sum_{i=1}^nx_iy_i\right|\le\sqrt{\sum_{i=1}^nx_i^2}\sqrt{\sum_{i=1}^nx_i^2} $$
5. Norma zadaje odległość (metrykę) wzorem $d(\vec{x},\vec{y}) = |\!|\vec{x} - \vec{y}|\!|$.
6. Nierówność trójkąta: $|\!|\vec{x}|\!|+|\!|\vec{y}|\!| \le |\!|\vec{x}+\vec{y}|\!|$.
7. Def. Mówimy, że wektory $\vec{x},\ \vec{y}$ są prostopadłe, jeśli $\langle\vec{x},\vec{y}\rangle=0$.
8. Twierdzenie Pitagorasa: Jeśli wektory $\vec{x},\ \vec{y}$ są prostopadłe, to $|\!|\vec{x}|\!|^2+|\!|\vec{y}|\!|^2=|\!|\vec{x}+\vec{y}|\!|^2$.

Lista zadań: ZSA_KI_LO_2015_W2.pdf.

Przestrzenie metryczne

• Data: 16.11.2015
• Wykładowca: dr Krzysztof Majcher

1. Dla niepustego zbioru $X$ funkcję $ d: X \times X \rightarrow \mathbb{R}$ nazywamy metryką jeśli dla dowolnych $x,y,z \in X$ spełnione są warunki:
   • $d(x,y) = 0$ wtedy i tylko wtedy, gdy $x=y$,
   • $d(x,y) = d(y,x)$,
   • $d(x,z) \leq d(x,y)+d(y,z)$.
   Zbiór $X$ wraz z funkcją $d$ spełniające powyższe warunki nazywamy przestrzenią metryczną i oznaczamy $(X,d)$.
   
2. Twierdzenie. Metryka przyjmuje wartości nieujemne.
3. Przykłady metryk na $\mathbb{R}^2$:
   • metryka euklidesowa
   • metryka miasto
   • metryka rzeka
4. Kulą domkniętą o środku w $x \in X$ i promieniu $r$, w przestrzeni metrycznej $(X,d)$ nazywamy zbiór $$ \{z \in X: d(x,z) \leq r \}.$$
5. Średnicą zbioru $A \subseteq X$ nazywamy liczbę rzeczywistą: $$diam(A)= \left\{\begin{array}{lcl} \sup \{ d(x,y): x,y \in A \}&:&A \neq \emptyset\\ 0&:&A = \emptyset \end{array} \right. $$
6. Twierdzenie Jeśli $\langle \cdot, \cdot \rangle : \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}$ jest iloczynem skalarnym, to funkcja $d(v,w)=\sqrt{\langle v-w,v-w \rangle}$ jest metryką na przestrzeni $\mathbb{R}^n$.

Lista zadań: ZSA_KI_LO_2015_W3.pdf.

Dyskretne przestrzenie metryczne

• Data: 30.11.2015
• Wykładowca: dr Robert Rałowski

• Niech $(X,d)$ będzie przestrzenią metryczną oraz $U\subseteq X$. $ U\text{ jest zbiorem otwartym w } X \text{ wtedy gdy } (\forall x\in U)(\exists r>0)\; ( K(x,r)\subseteq U). $
• Twierdzenie. Niech $(X,d)$ będzie przestrzenią metryczną. Wtedy
  1. $\emptyset, X$ są zbiorami otwartymi w $X$
  2. $U,V$ są otwarte w $X$, to $U\cup V$ jest również zbiorem otwartym w $X$
  3. suma dowolnej rodziny zbiorów otwartych w $X$ jest zbiorem otwartym w $X$.
• Definicja. Przestrzeń metryczna $X,d$ jest dyskretna (topologicznie) jeżeli każdy jej podzbiór jest zbiorem otwartym.
• Twierdzenie. Przestrzeń $(X,d)$ jest dyskretna wtedy i tylko wtedy, gdy każdy podzbiór jednopunktowy jest zbiorem otwartym.
• Przykłady:
1. $(X,d)$ - przestrzeń metryczna taka, że $X$ jest niepustym zbiorem skończonym,
2. $(X,d)$, dzie $X$ jest dowolnym niepustym zbiorem z metryką dyskretną tzn. z metryką zadaną wzorem $$ d(x,y)= \begin{cases} 1&:& x\ne y\\ 0&:& x=y \end{cases}~, $$ dla $x,y \in X$.
3. $X=\big\{\frac{1}{n+1}:\; n\in\mathbb{N}\big\}$ i $d(x,y)=|x-y|$ dla każdego $x,y\in X$
• Grafem nazywamy parę $\Gamma=(V,E)$, jeżeli $V$ jest niepustym zbiorem i $E\subseteq \{ A\subseteq V:\; moc(A)=2\}$, $V$ jest zbiorem wierzchołków a $E$ jest zbiorem wszystkich krawędzi w grafie $\Gamma$.
• Dla różnych wierzchołków $a,b\in V$ ciąg $(u_1,\ldots,u_n)$ jest ścieżką z $a$ do $b$ gdy
  1. $u_1=a$,
  2. $u_n=b$,
  3. $(\forall k\in\{1,\ldots,n-1\})(\{u_k,u_{k+1}\}\in E)$.
  Graf $(V,E)$ nazywamy grafem spójnym, gdy dla dowolnych różnych $a,b\in V$ istnieje ścieżka z $a$ do $b$.
• Niech $\Gamma=(V,E)$ będzie spójnym, skończonym grafem, to dla dowolnych $x,y\in V$ definiujemy metrykę następująco $$ d_\Gamma (x,y)=\begin{cases} \min\left\{ n-1:\; n\in\mathbb{N}\setminus\{0\}\, \land\, (v_1,\ldots,v_n)\text{ jest ścieżką od } \text{ do } y\right\} &:&x\ne y \\ 0 &:& x=y \end{cases} $$
• Twierdzenie. Jeżeli $V$ jest niepustym, skończonym zbiorem, $\Gamma=(V,E)$ jest grafem spójnym, to $(V,d_\Gamma)$ jest dyskretną przestrzenią metryczną.
  Dowód. Oczywiście funkcja $d_\Gamma$ jest nieujemna i wprost z definicji widać, że $d_\Gamma(x,y)=0$ wtedy i tylko wtedy gdy $x=y$.
  Aby wykazać symetrię, dla dowolnie wybranych dwóch różnych wierzchołków $x,y\in V$ wybierzmy ścieżkę $(v_1,\ldots, v_n)$ z $x$ do $y$, taką że $d_\Gamma(x,y)=n-1$. Wówczas $(v_n,v_{n-1},\ldots,v_1)$ jest ścieżką z $y$ do $x$, więc $d_\Gamma(y,x) \leq n-1 = d_\Gamma(x,y)$. Podobnie pokazujemy, że $d_\Gamma(x,y)\leq d_\Gamma(y,x)$. Zatem $d_\Gamma(y,x) = d_\Gamma(x,y)$
  
  Nierówność trójkąta dowodzimy w sposób następujący: Niech $x,y,z\in V$ będą dowolnymi wierzchołkami w grafie, niech $(v_1,\ldots,v_m)$ będzie ścieżką z $x$ do $z$ taką, że $d_\Gamma(x,z)=m-1$, oraz niech $(u_1,\ldots,u_k)$ będzie ścieżką od $z$ do $y$ taką, że $d_\Gamma(z,y)=k-1$. Wtedy oczywiście $(v_1,\ldots,v_m,u_2,\ldots u_k)$ jest ścieżką od $x$ do $y$ (tutaj $v_m=z$), a więc $$ d_\Gamma(x,y)\le (m+k-1)-1 =(m-1) + (k - 1) = d_\Gamma(x,z) + d_\Gamma(z,y). $$ Ponieważ $V$ jest zbiorem skończonym, więc $(V,d_\Gamma)$ jest dyskretna.

Lista zadań: ZSA_KI_LO_2015_W4

Liczby zespolone

• Data: 14.12.2015
• Wykładowca: dr Krzysztof Majcher

Liczbą zespoloną nazywamy wyrażenie postaci $a+bi$, gdzie $a$ i $b$ są liczbami rzeczywistymi, na przykład $3+5i$.
Zbiór $\mathbb{C}=\{a+bi: a,b \in \mathbb{R} \}$ nazywamy zbiorem liczb zespolonych.
Częścią rzeczywistą liczby zepolonej $z=a+bi$ nazywamy liczbę $\mathrm{Re}(z)=a$, natomiast częścią urojoną nazywamy liczbę $\mathrm{Im}(z)=b$.

Działania na liczbach zespolonych

• dodawanie: $(a+bi)+ (c+di)=(a+c)+(b+d)i$
• odejmowanie: $(a+bi)- (c+di)=(a-c)+(b-d)i$
• mnożenie: $(a+bi) (c+di)=(ac-bd)+(ad+cb)i$
• dzielenie: $\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)} =\frac{(a+bi)(c-di)}{c^2+d^2}=\ldots$

Patrz: Aplety

Interpretacja geometryczna

Liczbę zespoloną $z=a+bi$ interpretujemy jako punkt o współrzędnych $(a,b)$ na płaszczyźnie.

Postać trygonometryczna

$$ z=r\cdot(\cos\alpha +i \sin\alpha) $$ Wzór de Moivre'a: $$ \big(r\cdot(\cos\alpha +i \sin\alpha)\big) \cdot \big(s\cdot(\cos\beta +i \sin\beta)\big) = (r\cdot s)\cdot(\cos(\alpha+\beta) +i \sin(\alpha+\beta)) $$

Lista zadań: ZSA_KI_LO_2015_W5.pdf.

Liczby całkowite

• Data: 04.01.2016
• Wykładowca: dr hab. Marek Klonowski

Definicja Mówimy, że liczba całkowita $b$ jest podzielna przez pewną liczbę całkowitą $a\neq b$ jeżeli istnieje liczba całkowita $k$, taka że $b=k\cdot a$.
Mówimy też, że liczba $a$ dzieli $b$ i oznaczamy przez symbol $a\mid b$. Jeśli liczba $a$ nie dzieli $b$ to piszemy $a \not\mid b$
Twierdzenie Niech $a,b,c \in \mathbb{Z}$ oraz $a,b \neq 0$. Wtedy

1. $(a\mid b) \Rightarrow (\forall c \in \mathbb{Z})( a\mid b\cdot c )$
2. $((a\mid b) \land (b\mid c)) \Rightarrow (a \mid c)$
3. $((a\mid b )\land (a\mid c)) \Rightarrow (\forall x,y \in \mathbf{Z})( a \mid (b\cdot x + c\cdot y))$

Twierdzenie Dla dowolnej liczby całkowitej $b$ i dowolnego $a\neq 0$ istnieją liczby całkowite $k,r$, takie że $b= k\cdot a + r$ oraz $0\leq r < |a|$. Liczbę $r$ nazywamy resztą z dzielenia $b$ przez $a$.

Definicja $\mathrm{NWD}(a,b) = \max \{c\in \mathbb{Z} : c \mid a \wedge c \mid b \}$

Definicja (Kongruencje) $a,b \in \mathbb{Z}$ Mówimy, że liczby $a$ i $b$ przystają do siebie modulo $m$ jeśli $m \mid (a-b)$. Oznaczamy to $a \equiv_{m} b$.

Lista zadań: ZSA_KI_LO_2015_W6.pdf.

Ciała liczbowe $\mathbb{Z}_p$

• Data: 18.01.2016
• Wykładowca: dr Robert Rałowski

• Kongruencja. Niech $x,y\in\mathbb{Z}$ i $n\in\mathbb{N}\setminus\{0\}$. $$ (x\equiv y \mod n) \iff (n|(x-y)) \iff (\exists k\in\mathbb{Z}) (x-y = k\cdot n)~. $$
• Twierdzenie. Dla dowolnych liczb $a,b,c,d\in\mathbb{Z}$ i dowolnej dodatniej liczby naturalnej $n\in\mathbb{N}\setminus\{0\}$ mamy:
  1. $a\equiv a \mod n$
  2. $(a\equiv b \mod n) \longrightarrow (b\equiv a\mod n)$,
  3. $(a\equiv b\mod n) \land (b\equiv c\mod n) \longrightarrow (a\equiv c\mod n)$,
  4. $(a\equiv b\mod n)\land (c\equiv d\mod n) \longrightarrow ((a+c)\equiv (b+d)\mod n)$.
  5. $(a\equiv b\mod n) \land (c\equiv d\mod n)\longrightarrow ((a\cdot c)\equiv (b\cdot d)\mod n) $,
  6. Jeśli $\mathrm{NWD}(a,n)=1$, to $(ab\equiv ac\mod n) \longrightarrow (b\equiv c \mod n)$,
  7. $(\forall x\in\mathbb{Z})(\exists! r\in\{0,1,\ldots,n-1\})\; x\equiv r\mod n$;
     liczbę $(x)_n=r$ nazywamy resztą z dzielenia liczby $x$ przez $n$.
• Definicja zbioru $\mathbb{Z}_n.$ Dla dowolnej dodatniej liczby naturalnej $n$ definiujemy zbiór $\mathbb{Z}_n=\{ k\in\mathbb{Z}:\; 0\le k < n\}=\{ 0,1,\ldots,n-1 \}.$
• Działania w zbiorze $\mathbb{Z}_n.$. Dla dowolnych $x,y\in\mathbb{Z}_n$ definiujemy
  • $x +_n y = (x + y)_n\in\mathbb{Z}_n$,
  • $x \cdot_n y = (x \cdot y)_n\in\mathbb{Z}_n$.
• Twierdzenie. Dla dowolnej dodatniej liczby naturalnej $n\in\mathbb{N}\setminus\{0,1\}$ mamy
  • $(\forall x,y,z\in\mathbb{Z}_n)\left( (x +_n y) +_n z = x +_n (y +_n z)\right)$,
  • $(\forall x,y\in\mathbb{Z}_n)\left( x +_n y = y +_n x\right)$,
  • $(\forall x\in\mathbb{Z}_n)\left( x +_n 0 = x = 0 +_n x\right)$,
  • $(\forall x\in\mathbb{Z}_n)(\exists y\in\mathbb{Z}_n)\left( x +_n y = 0 = y +_n x\right)$,
  • $(\forall x,y,z\in\mathbb{Z}_n)\left( (x \cdot_n y) \cdot_n z = x \cdot_n (y \cdot_n z)\right)$,
  • $(\forall x,y\in\mathbb{Z}_n)\left( x \cdot_n y = y \cdot_n x\right)$,
  • $(\forall x\in\mathbb{Z}_n)\left( x \cdot_n 1 = x = 1 \cdot_n x\right)$,
  • $(\forall x,y,z\in\mathbb{Z}_n)\left( (x +_n y) \cdot_n z = (x \cdot_{n} z) +_n (y \cdot_{n} z) \right)$.
• Twierdzenie Eulera Dla dowolnych $a\in\mathbb{Z}$, $n\in\mathbb{N}\setminus\{ 0,1\}$, jeżeli liczby $a$, $n$ są względnie pierwsze, to $a^{\varphi(n)} \equiv 1 \mod n,$
  gdzie $\varphi(n) = \text{ moc } \{ k\in \mathbb{N}\setminus \{ 0\}: NWD(k,n) = 1\}$ jest funkcją Eulera.
• Twierdzenie. Funkcja Eulera ma następujące własności:
  • $p$-liczba pierwsza to $\varphi(p^n)=p^n-p^{n-1}$,
  • $k,l$ są względnie pierwsze to $\varphi(kl) = \varphi(k)\varphi(l)$.
• Twierdzenie (małe twierdzenie Fermata) Niech $p$ będzie liczbą pierwszą oraz $a\in\mathbb{Z}$. Jeżeli $p$ nie dzieli $a$, to $a^{p-1} \equiv 1 \mod p$.
• Definicja (Ciało). Uporządkowaną piątkę $(K,+,\cdot,0,1)$ nazywamy ciałem jeżeli są spełnione następujące werunki:
  1. $K$ ma przynajmniej dwa elementy,
  2. $+:K\times K \to K$, $\cdot:K\times K\to K$ są działaniami dwuargemontowymi, (zamiast pisać $+(x,y)$, $\cdot (x,y)$ piszemy $x + y$ i $x \cdot y$),
  3. $(\forall x,y,z\in K)( (x + y) + z = x + (y + z))$,
  4. $(\forall x,y\in K) (x + y = y + x)$,
  5. $(\forall x\in K)( x + 0 = x = 0 + x)$,
  6. $(\forall x\in K)(\exists y\in K)( x + y = 0 = y + x)$,
  7. $(\forall x,y,z\in K\setminus\{0\})( (x \cdot y) \cdot z = x \cdot (y \cdot z))$,
  8. $(\forall x,y\in K\setminus\{0\})( x \cdot y = y \cdot x)$,
  9. $(\forall x\in K\setminus\{0\})( x \cdot 1 = x = 1 \cdot x)$,
  10. $(\forall x\in K\setminus\{0\})(\exists y\in K\setminus\{0\})( x \cdot y = 1 = y \cdot x )$,
  11. $(\forall x,y,z\in K)( (x + y) \cdot z = (x \cdot z) + (y \cdot_n z))$.
• Przykłady:
  1. ciało liczb wymiernych $(\mathbb{Q},+\cdot,0,1)$,
  2. ciało liczb rzeczywistych $(\mathbb{R},+\cdot,0,1)$,
  3. ciało liczb zespolonych $(\mathbb{C},+\cdot,0,1)$,
  4. $(\mathcal{W},+\cdot,0,1)$, gdzie $a\in\mathbb{R}$ jest liczbą przestępną (czyli nie jest liczbą algebraiczną) oraz $$\mathcal{W} = \bigg\{ \frac{f(a)}{g(a)}:\;\; f,g\in\mathbb{Z}[x]\land g\ne0 \bigg\}.$$
• Twierdzenie. Dla każdej liczby naturalnej $n>1$ następujące dwa zdania są równoważne:
  1. $(\mathbb{Z}_n,+_n,\cdot_n,0,1)$ jest ciałem
  2. $n$ jest liczbą pierwszą.

Lista zadań: ZSA_KI_LO_2015_W7.pdf.