fd_labeling/1

Rozpatrzmy problem generowania permutacji.

O permutacjach liczb od 1 do N wiemy, że:

• składają się z N elementów;
• każdy element jest liczbą całkowitą z zakresu 1..N;
• wszystkie elementy są parami różne.
  

Zapiszmy to w postaci predykatu perm/2, którego pierwszym argumentem jest długość permutacji N, natomiast drugim jest permutacja P:

perm(N, P) :-
     length(P, N),
     fd_domain(P, 1, N),
     fd_labeling(P),
     fd_all_different(P).

Pierwszy warunek length(P, N) wyraża, że szukana permutacja P jest listą złożoną z N elementów. Dwa następne warunki fd_domain(P, 1, N) i fd_labeling(P) ograniczają zbiór możliwych wartości każdego z elementów do zakresu 1..N i podstawiają pod każdy z elementów listy P wartość z tego zakresu. Ostatni warunek wyraża, że żadna z wartości na liście P nie może się powtórzyć.

Sprawdźmy jak wygląda permutacja liczb od 1 do 10:

| ?- perm(10, X).

X = [1,2,3,4,5,6,7,8,9,10] ?

(30516 ms) yes

Hmm... ponad trzydzieści sekund trwało wygenerowanie pierwszej z ponad trzech milionów permutacji. Gdzie popełniliśmy błąd?

Otóż powyższy predykat zupełnie nie wykorzystuje mocy jaką dostarcza technologia więzów. Jest on napisany zgodnie z klasyczną w Prologu zasadą generuj i testuj, tzn. najpierw generuje całą listę P a następnie sprawdza za pomocą predykatu fd_all_different/1 czy wygenerowana lista jest poprawną permutacją.

Dla uproszczenia analizy przyjmijmy, że N=3.

Niech P będzie listą złożoną z trzech zmiennych P1, P2, P3. Po zdefiniowaniu zakresów dla tych zmiennych, predykat fd_labeling/1 przystępuje do podstawiania pod kolejne zmienne wartości z ich dziedzin.

Przy pierwszym podstawieniu, zmienne [P1, P2, P3] przyjmą wartości [1, 1, 1], jednak to podstawienie zostanie odrzucone przez warunek fd_all_different/1.

Kolejnym podstawieniem znalezionym przez fd_labeling/1 są wartości [1, 1, 2] ale i one zostają odrzucone.

Poniżej wypisane są wszystkie kolejno odrzucane przez warunek fd_all_different/1 podstawienia:

[1, 1, 1]
[1, 1, 2]
[1, 1, 3]
[1, 2, 1]
[1, 2, 2]

Dopiero szóste podstawienie [1, 2, 3] zostaje zaakceptowane:



W przypadku N=10, predykat fd_all_different/1 odrzuca:

• 100,000,000 podstawień, w których P1=1, P2=1;
• 10,000,000 podstawień, w których P1=1, P2=2, P3=1;
• 10,000,000 podstawień, w których P1=1, P2=2, P3=3;
• 1,000,000 podstawień, w których P1=1, P2=2, P3=3, P4=1;
• 1,000,000 podstawień, w których P1=1, P2=2, P3=3, P4=2;
• 1,000,000 podstawień, w których P1=1, P2=2, P3=3, P4=3;
• ...
• 1 podstawienie, w których P1=1, P2=2, P3=3, P4=4, P5=5, P6=6, P7=7, P8=8, P9=9, P10=9.

Łącznie jest odrzuconych 123,456,789 podstawień zanim zostanie zaakceptowane rozwiązanie [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] i stąd tak długi czas jego poszukiwania.

Aby przyspieszyć predykat perm/2 należy skorzystać z najważniejszej zasady stosowanej w technologii więzów:

Zanim przystąpisz do podstawiania wartości za zmienne, narzuć na te zmienne wszystkie ograniczenia.

Warunek fd_all_different/1 jest ograniczeniem na zmienne występujące na liście P, więc powinien wystąpić przed podstawieniami.

Oto druga, szybsza, wersja predykatu generującego permutacje:

perm2(N, P) :-
     length(P, N),
     fd_domain(P, 1, N),
     fd_all_different(P),
     fd_labeling(P).

Tym razem potrzeba czasu krótszego niż jedna milisekunda na wygenerowanie pierwszej permutacji:

| ?- perm2(10, X).

X = [1,2,3,4,5,6,7,8,9,10] ?

yes

Natomiast wszystkie 3,628,800 permutacji zostaje wygenerowanych w niecałe 3.5 sekundy:

| ?- perm2(10, _), fail.

(3277 ms) no

Na działanie predykatu fd_labeling/1 można patrzeć jak na przeszukiwanie wgłąb pewnego drzewa.

Przeszukiwanie drzewa w przypadku N = 3, gdy wcześniej narzucono warunek fd_all_different/1, przedstawiono na poniższym rysunku: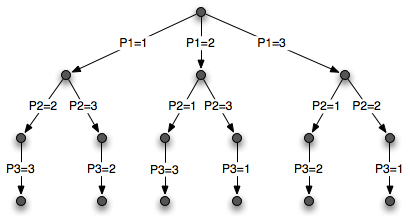



Przeszukiwanie odbywa się kolejnymi gałęziami od lewej do prawej strony. Wynika to z tego, że wartości z zakresu podanego dla każdej zmiennej wybierane są od najmniejszej do największej.

Znalezienie rozwiązania ma miejsce po dojściu do liścia. Następne odpowiedzi znajduje się wywołując nawrót i zmuszając predykat fd_labeling/1 do wycofania się w algorytmie przeszukiwania wgłąb.

Nawroty można uzyskiwać również naciskając średnik po każdej odpowiedzi:

| ?- perm2(3, X).

X = [1,2,3] ? ;

X = [1,3,2] ? ;

X = [2,1,3] ? ;

X = [2,3,1] ? ;

X = [3,1,2] ? ;

X = [3,2,1]

(1 ms) yes

albo drukując odpowiedź i wywołując warunek fail/0, który zawsze kończy się niepowodzeniem i powoduje nawrót:

| ?- perm2(3, X), write(X), nl, fail.
[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]

no

Przy wywołaniu predykatu fd_labeling można podać jeszcze drugi parametr, który odpowiednio sterując procesem przeszukiwania drzewa może w istotny sposób przyspieszyć czas znajdowania rozwiązywania.

Więcej o tym przy opisie predykatu fd_labeling/2.

Tags: gnu-prolog