Algorytm = Logika + Sterowanie
fd_labeling/2
18/03/08 12:00
W notatce poświęconej predykatowi fd_labeling/1 przedstawiono predykat generujący permutacje liczb od 1 do N.
Wykorzystamy ten predykat do znajdowania rozmieszczenia N niebijących się nawzajem hetmanów na szachownicy rozmiaru NxN (o ustawianiu hetmanów można poczytać tutaj).
W poniższym predykacie hetmany/2 umieszczono przed etykietowaniem zmiennych (podstawianiem wartości) dodatkowy warunek zapewniający, że żadne dwa hetmany, ustawione zgodnie z permutacją P, nie biją się po przekątnej:
hetmany(N, P) :-
length(N, P),
fd_domain(P, 1, N),
dobra(P),
fd_labeling(P).
dobra([]).
dobra([X | L]) :-
dobra(L, X, 1),
dobra(L).
dobra([], _, _).
dobra([Y | L], X, K) :-
X+K #\= Y,
X #\= Y+K,
K1 is K+1,
dobra(L, X, K1).
Gdy podstawianie wartości odbywa się przy użyciu predykatu fd_labeling/1, wtedy zmienne podstawiane są w takiej kolejności w jakiej występują na liście P, tzn. P1, P2, ..., Pn, oraz w kolejnych próbach podstawiane są pod nie wartości 1, 2, ..., N, tj. od najmniejszej do największej.
Na poniższym rysunku przedstawiono proces poszukiwania rozwiązania w przypadku N=6:
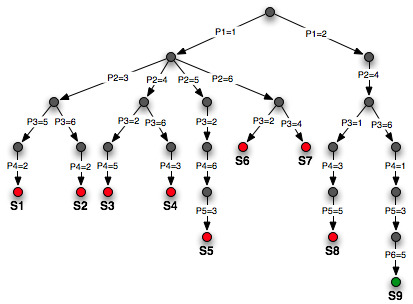
Jak widać, osiem ścieżek zakończyło się niepowodzeniem (sytuacje S1, S2, ..., S8), natomiast dopiero dziewiąta ścieżka doprowadziła do ustawienia wszystkich sześciu hetmanów (sytuacja S9).
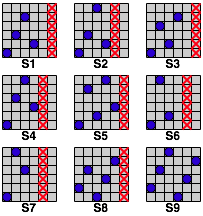
Sytuacje S1-S9 przedstawiono na poniższym rysunku:
Liczba ścieżek zakończonych niepowodzeniem przed znalezieniem rozwiązania nazywa się liczbą nawrotów (ang. backtracks).
W wywołaniu predykatu fd_labeling/2 można jako drugi argument podać listę opcji:
fd_labeling(+ListaFDzmiennych, +ListaOpcji).
Jedną z opcji jest term backtracks(B), gdzie B jest zmienną pod którą zostanie podstawiona liczba nawrotów jaka potrzebna była do znalezienia rozwiązania.
Gdy zmienne etykietuje się po kolei a wartości podstawiane są od najmniejszej do największej, to do znalezienia ustawienia sześciu hetmanów potrzeba ośmiu nawrotów. Jednak do ustawienia 30 hetmanów potrzeba w ten sposób ponad 7 milionów nawrotów!
Aby przyspieszyć poszukiwanie rozwiązania, tj. zmniejszyć liczbę nawrotów, można zastosować heurystykę wyboru zmiennej oraz heurystykę wyboru wartości.
Heurystykę wyboru zmiennej określa się podając w drugim parametrze predykatu fd_labeling opcję variable_method(H), gdzie H jest nazwą jednej z dostępnych heurystyk:
Na liczbę nawrotów ma również wpływ kolejność wyboru wartości podstawianych pod zmienną. Zadaje się nią w drugim parametrze predykatu fd_labeling podając opcję value_method(H), gdzie H jest jedną z heurystyk:
W poniższej tabeli dokonano porównania liczby nawrotów w przypadku zastosowania różnych heurystyk i dla różnego rozmiaru problemu (liczby ustawianych hetmanów):
__N_______brak___middle_________ff__ff+middle
_10_________24________2__________9__________0
_20_____37,320_______38_________26__________2
_30__7,472,978______169________127_________35
_40_____________406,195_________22_________50
_50__________________________8,891__________0
_60____________________________224__________8
_70__________________________8,941________117
_80_________________________68,064__________0
_90______________________1,935,628_________48
100_________________________24,345__________1
Powyższe wyniki zebrano na wykresie:
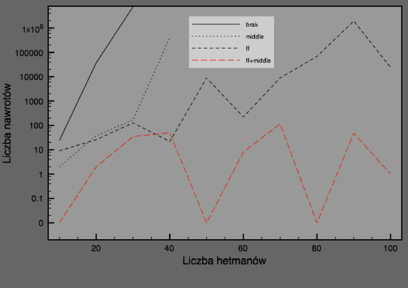
Jak widać, przy tym samym rozmiarze problemu, można zmniejszyć liczbę nawrotów nawet setki tysięcy razy przez odpowiedni dobór heurystyk sterujących pracą predykatu fd_labeling/2.
Opierając się na powyższych wynikach eksperymentów, można zaproponować następującą wersję predykatu hetmany/2:
hetmany(N, P) :-
length(P, N),
fd_domain(P, 1, N),
fd_all_different(P),
dobra(X),
fd_labeling(P, [
variable_method(ff),
value_method(middle)]).
Jeśli żadna z dostępnych heurystyk nie zmniejszy liczby nawrotów w stopniu, który umożliwia rozwiązanie jakiegoś problemu w akceptowalnym czasie, to zawsze można próbować zastąpić predykat fd_labeling/2 własnym predykatem, który dokonuje etykietowania w odpowiedniejszy sposób, zależny od własności rozwiązywanego problemu. Wymaga to jednak dokładnego zbadania problemu i opracowania takiego wyspecjalizowanego sposobu etykietowania.
Wykorzystamy ten predykat do znajdowania rozmieszczenia N niebijących się nawzajem hetmanów na szachownicy rozmiaru NxN (o ustawianiu hetmanów można poczytać tutaj).
W poniższym predykacie hetmany/2 umieszczono przed etykietowaniem zmiennych (podstawianiem wartości) dodatkowy warunek zapewniający, że żadne dwa hetmany, ustawione zgodnie z permutacją P, nie biją się po przekątnej:
hetmany(N, P) :-
length(N, P),
fd_domain(P, 1, N),
dobra(P),
fd_labeling(P).
dobra([]).
dobra([X | L]) :-
dobra(L, X, 1),
dobra(L).
dobra([], _, _).
dobra([Y | L], X, K) :-
X+K #\= Y,
X #\= Y+K,
K1 is K+1,
dobra(L, X, K1).
Gdy podstawianie wartości odbywa się przy użyciu predykatu fd_labeling/1, wtedy zmienne podstawiane są w takiej kolejności w jakiej występują na liście P, tzn. P1, P2, ..., Pn, oraz w kolejnych próbach podstawiane są pod nie wartości 1, 2, ..., N, tj. od najmniejszej do największej.
Na poniższym rysunku przedstawiono proces poszukiwania rozwiązania w przypadku N=6:

Jak widać, osiem ścieżek zakończyło się niepowodzeniem (sytuacje S1, S2, ..., S8), natomiast dopiero dziewiąta ścieżka doprowadziła do ustawienia wszystkich sześciu hetmanów (sytuacja S9).
Sytuacje S1-S9 przedstawiono na poniższym rysunku:

Liczba ścieżek zakończonych niepowodzeniem przed znalezieniem rozwiązania nazywa się liczbą nawrotów (ang. backtracks).
W wywołaniu predykatu fd_labeling/2 można jako drugi argument podać listę opcji:
fd_labeling(+ListaFDzmiennych, +ListaOpcji).
Jedną z opcji jest term backtracks(B), gdzie B jest zmienną pod którą zostanie podstawiona liczba nawrotów jaka potrzebna była do znalezienia rozwiązania.
Gdy zmienne etykietuje się po kolei a wartości podstawiane są od najmniejszej do największej, to do znalezienia ustawienia sześciu hetmanów potrzeba ośmiu nawrotów. Jednak do ustawienia 30 hetmanów potrzeba w ten sposób ponad 7 milionów nawrotów!
Aby przyspieszyć poszukiwanie rozwiązania, tj. zmniejszyć liczbę nawrotów, można zastosować heurystykę wyboru zmiennej oraz heurystykę wyboru wartości.
Heurystykę wyboru zmiennej określa się podając w drugim parametrze predykatu fd_labeling opcję variable_method(H), gdzie H jest nazwą jednej z dostępnych heurystyk:
- standard - zmienne wybierane w kolejności występowania na liście (domyślna kolejność);
- first_fail (albo ff) - w pierwszej kolejności wybierana jest zmienna o najmniejszej liczbie wartości w dziedzinie;
- most_constrained - podobnie jak w przypadku first_fail ale jeśli dwie zmienne mają ten sam rozmiar dziedziny, to wybierana jest zmienna występująca w większej licznie ograniczeń;
- smallest - w pierwszej kolejności wybierana jest zmienna o najmniejszej wartości w swojej dziedzinie, przy czym jeśli dwie zmienne mają tę samą najmniejszą wartość, to wybierana jest zmienna występująca w większej liczbie ograniczeń;
- largest - podobnie jak w przypadku smallest z tą różnicą, że zmienne wybierane są w malejącej kolejności największych wartości w dziedzinach;
- max_regret - wybierana jest zmienna o największej różnicy między najmniejszą a kolejną wartością w dziedzinie, przy czym jeśli dwie zmienne mają taką samą największą tę różnicę, to wybierana jest ta zmienna, która występuje w większej liczbie ograniczeń;
- random - zmienne wybierane są w losowej kolejności.
Na liczbę nawrotów ma również wpływ kolejność wyboru wartości podstawianych pod zmienną. Zadaje się nią w drugim parametrze predykatu fd_labeling podając opcję value_method(H), gdzie H jest jedną z heurystyk:
- min - wartości wybierane są od najmniejszej do największej;
- max - wartości wybierane są od największej do najmniejszej;
- middle - wartości wybierane są od środkowej w dziedzinie ku jej brzegom;
- random - wartości wybierane są w losowej kolejności.
W poniższej tabeli dokonano porównania liczby nawrotów w przypadku zastosowania różnych heurystyk i dla różnego rozmiaru problemu (liczby ustawianych hetmanów):
__N_______brak___middle_________ff__ff+middle
_10_________24________2__________9__________0
_20_____37,320_______38_________26__________2
_30__7,472,978______169________127_________35
_40_____________406,195_________22_________50
_50__________________________8,891__________0
_60____________________________224__________8
_70__________________________8,941________117
_80_________________________68,064__________0
_90______________________1,935,628_________48
100_________________________24,345__________1
Powyższe wyniki zebrano na wykresie:

Jak widać, przy tym samym rozmiarze problemu, można zmniejszyć liczbę nawrotów nawet setki tysięcy razy przez odpowiedni dobór heurystyk sterujących pracą predykatu fd_labeling/2.
Opierając się na powyższych wynikach eksperymentów, można zaproponować następującą wersję predykatu hetmany/2:
hetmany(N, P) :-
length(P, N),
fd_domain(P, 1, N),
fd_all_different(P),
dobra(X),
fd_labeling(P, [
variable_method(ff),
value_method(middle)]).
Jeśli żadna z dostępnych heurystyk nie zmniejszy liczby nawrotów w stopniu, który umożliwia rozwiązanie jakiegoś problemu w akceptowalnym czasie, to zawsze można próbować zastąpić predykat fd_labeling/2 własnym predykatem, który dokonuje etykietowania w odpowiedniejszy sposób, zależny od własności rozwiązywanego problemu. Wymaga to jednak dokładnego zbadania problemu i opracowania takiego wyspecjalizowanego sposobu etykietowania.